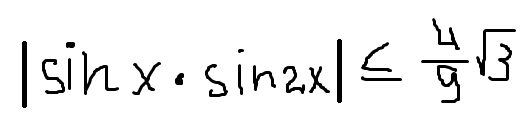Ответы
Ответ дал:
0
Доказательство:
Пусть
Вычислим значения функции в точке t
Поэтому,
Что и требовалось доказать
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад