Ответы
Ответ дал:
0
Угол В. равен 180-(90+30)=60.
Т.к. СН - это высота, то угол СНВ = 90.
Тогда угол НСВ=180-(90+60)=30
Напротив угла, равного 30, лежит сторона, равная половине гепат. ⇒ ВС=98:2=49. Тогда и напротив угла НСВ лежит сторона, равная половине гепат. ⇒ ВН=49:2=24,5
Ответ: ВН=24,5.
Т.к. СН - это высота, то угол СНВ = 90.
Тогда угол НСВ=180-(90+60)=30
Напротив угла, равного 30, лежит сторона, равная половине гепат. ⇒ ВС=98:2=49. Тогда и напротив угла НСВ лежит сторона, равная половине гепат. ⇒ ВН=49:2=24,5
Ответ: ВН=24,5.
Ответ дал:
0
свойства прямоугольного треугольника: 
Угол А=30, навпротив угла 30 катет ВС равен половине гипотенузе:

Ищем часть гипотенузы ВН

Ответ: 24.5
Угол А=30, навпротив угла 30 катет ВС равен половине гипотенузе:
Ищем часть гипотенузы ВН
Ответ: 24.5
Приложения:
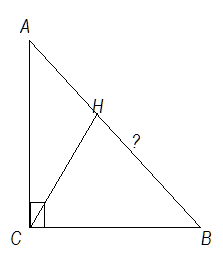
Вас заинтересует
2 года назад
2 года назад
10 лет назад
10 лет назад
10 лет назад