Ответы
Ответ дал:
0
Второе уравнение ......
Приложения:
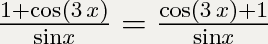

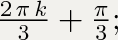
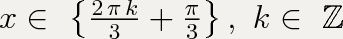
Ответ дал:
0
1) 2cosx + √3 = 0
2sinx + 1 ≠ 0
cosx = - √3 /2
x = (+ -)arccos(- √3/2) + 2πn, n∈Z
x = (+ -)(π - π/6) + 2πn, n∈Z
x = (+ -)(5π/6) + 2πn, n∈Z
2sinx + 1 ≠ 0
sinx ≠ 1/2
x ≠ (-1)^(n)arcsin(1/2) + πk, k∈Z
x ≠ (-1)^(n)(π/6) + πk, k∈Z
Ответ: x = (+ -)(5π/6) + 2πn, n∈Z; x ≠ (-1)^(n)(π/6) + πk, k∈Z
2) 1 + cos3x = 0
sinx ≠ 0
1 + cos3x = 0
cos3x = - 1
3x = π + 2πk, k∈Z
x = π/3 + 6πk, k∈z
sinx ≠ 0
x ≠ πn, n∈Z
Ответ: x = π/3 + 6πk, k∈z; x ≠ πn, n∈Z
2sinx + 1 ≠ 0
cosx = - √3 /2
x = (+ -)arccos(- √3/2) + 2πn, n∈Z
x = (+ -)(π - π/6) + 2πn, n∈Z
x = (+ -)(5π/6) + 2πn, n∈Z
2sinx + 1 ≠ 0
sinx ≠ 1/2
x ≠ (-1)^(n)arcsin(1/2) + πk, k∈Z
x ≠ (-1)^(n)(π/6) + πk, k∈Z
Ответ: x = (+ -)(5π/6) + 2πn, n∈Z; x ≠ (-1)^(n)(π/6) + πk, k∈Z
2) 1 + cos3x = 0
sinx ≠ 0
1 + cos3x = 0
cos3x = - 1
3x = π + 2πk, k∈Z
x = π/3 + 6πk, k∈z
sinx ≠ 0
x ≠ πn, n∈Z
Ответ: x = π/3 + 6πk, k∈z; x ≠ πn, n∈Z
Приложения:
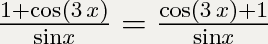

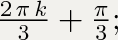
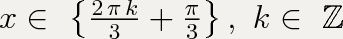
Вас заинтересует
2 года назад
10 лет назад
10 лет назад