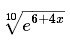Ответы
Ответ дал:
0
на рисунке только одна функция
Ответ дал:
0
первая (e^(6+4x))^(1/10) ' = 2/5*(e^(2x+3))^(1/5)
вторая (2/5*(e^(2x+3))^(1/5) ) ' = 4/25*(e^(2x+3))^(1/5)
третья (4/25*(e^(2x+3))^(1/5)) ' = 8/125*(e^(2x+3))^(1/5)
Вас заинтересует
2 года назад
2 года назад
8 лет назад
11 лет назад
11 лет назад
11 лет назад