Ответы
Ответ дал:
0
3)
lgxlgx=lg(10000)
lg"x=4 lgx=a
a"x=4
a=+2,-2
lgx=2 lgx= -2
10"=100 x=1/100
x=100
lgxlgx=lg(10000)
lg"x=4 lgx=a
a"x=4
a=+2,-2
lgx=2 lgx= -2
10"=100 x=1/100
x=100
Приложения:
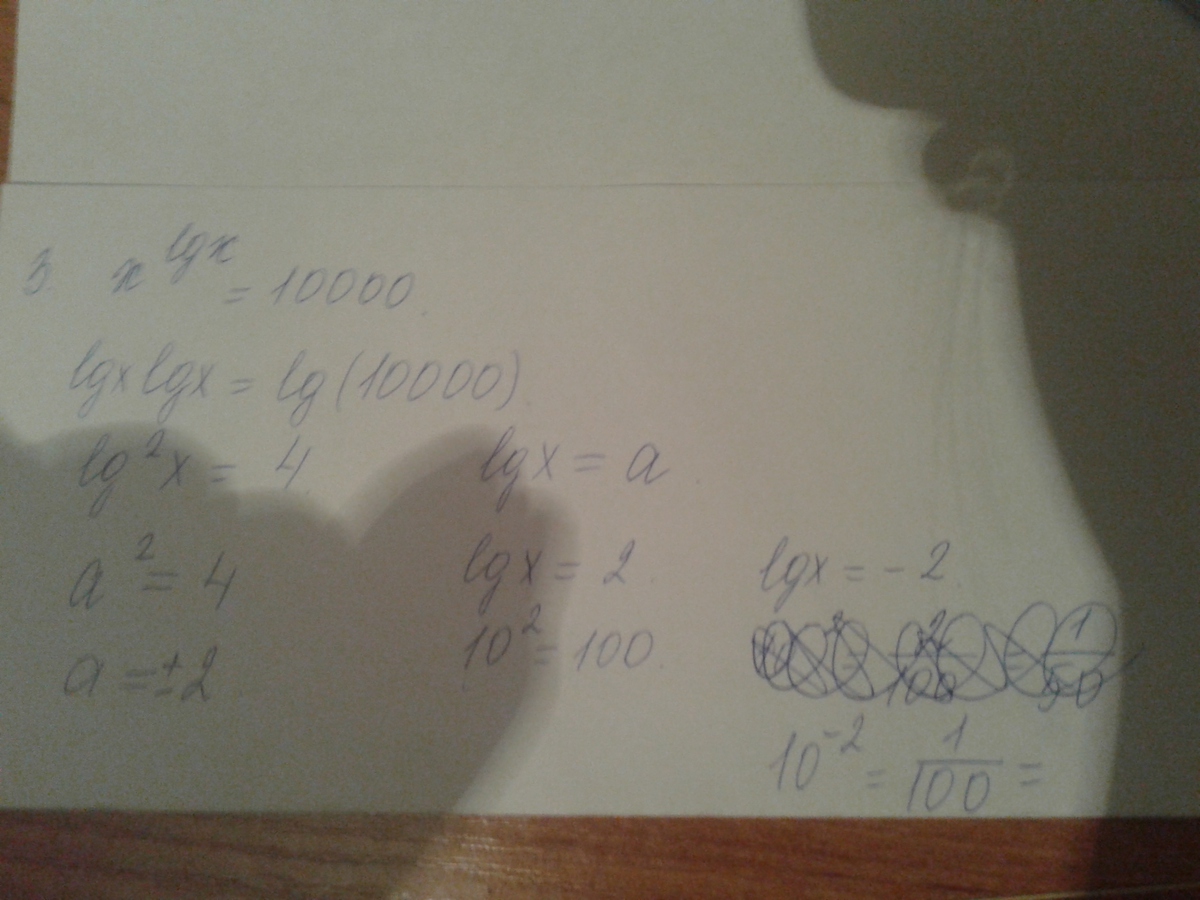
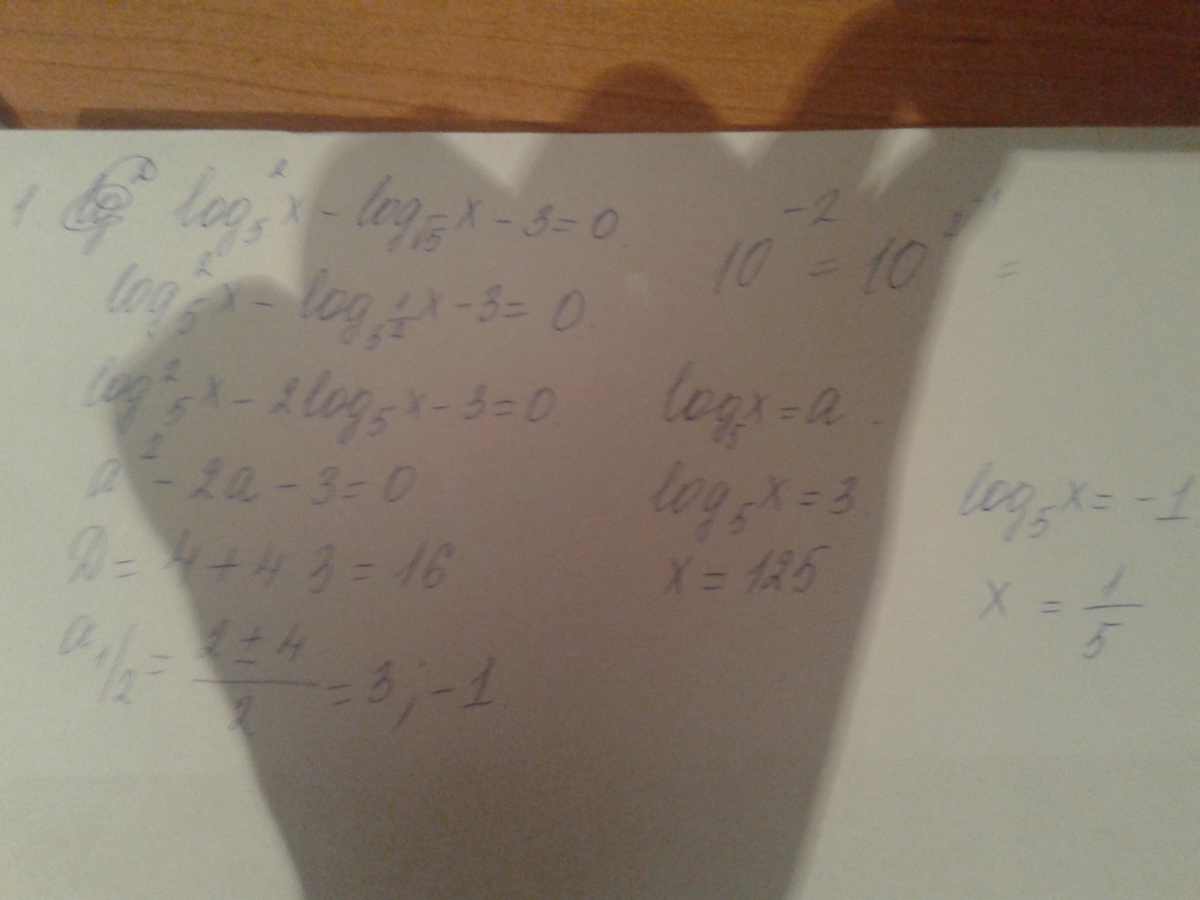
Ответ дал:
0
а можно на листочке просто не понятно
Ответ дал:
0
вот еще 1
Ответ дал:
0
Корни найдены по теореме Виета. Можно решить через дискриминант, но так будет дольше.
При всех x ОДЗ логарифма проходит, проверка не требуется.
Приложения:
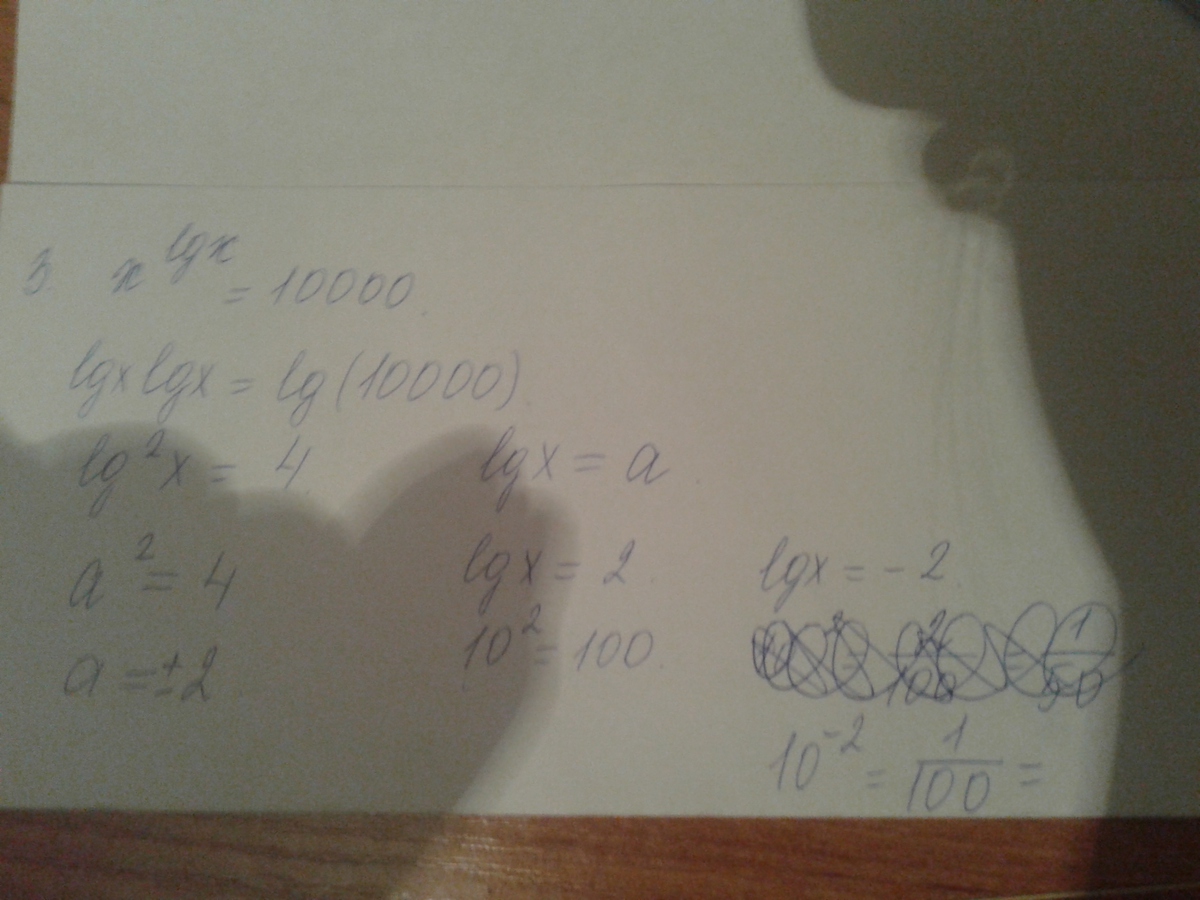
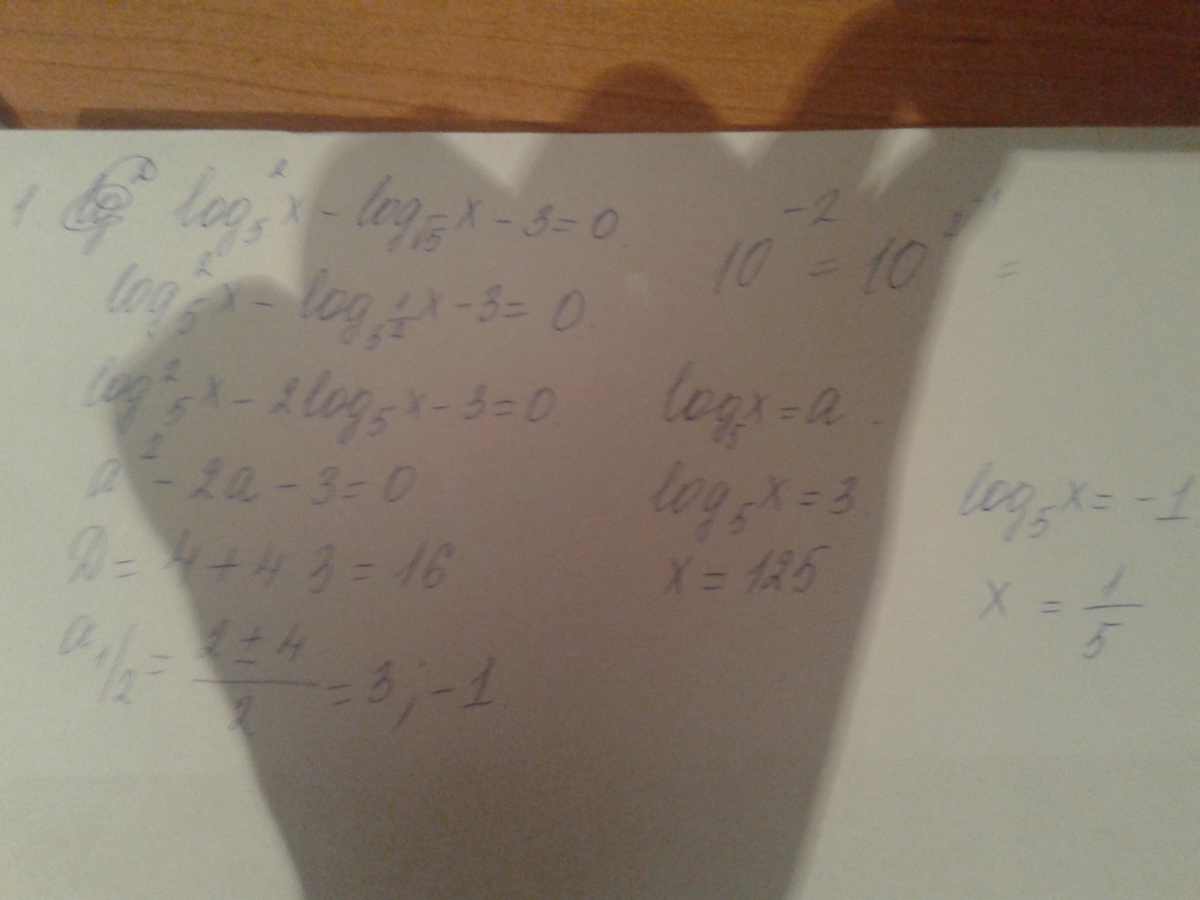
Ответ дал:
0
братан побратски на листик если не впадлу
Ответ дал:
0
Только 3 сделал
Ответ дал:
0
Сделал все номера. 3 и 1 почему-то идут рядом выше надписи про теорему Виета. Всё в картинках должно быть
Вас заинтересует
2 года назад
8 лет назад
10 лет назад
10 лет назад
