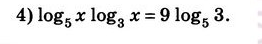Ответы
Ответ дал:
0
ОДЗ:
Воспользуемся формулами перехода к новому основанию
Система эквивалентна предыдущему
ПОсле упрощения выражения получаем
Ответ: 1; 19683.
Вас заинтересует
2 года назад
7 лет назад
10 лет назад
10 лет назад