Question

Все стороны квадрата, периметр которого равен 40 см, касаются сферы. найдите площадь сферы, если расстояние от её центра до плоскости квадрата равно
12 см.

Answer 1

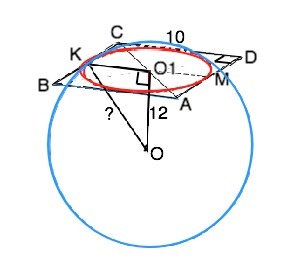
 Стороны квадрата АВСD касаются сферы. Линия пресечения сферы плоскостью квадрата - вписанная в него окружность с диаметром КМ, равным стороне этого квадрата. Р(АВСD)=40 см ⇒ АВ =10 см.Тогда радиус вписанной в квадрат окружности r=КО1=10:2=5 см. Расстояние от цента сферы до плоскости квадрата равно длине отрезка, проведенного перпендикулярно к точке пересечения его диагоналей ( к центру окружности сечения).

  Радиус сечения и расстояние от его центра до центра сферы - катеты прямоугольного треугольника КОО1, а радиус сферы КО - его гипотенуза. По т.Пифагора КО=√(KO²+OO1²)=13 см. Формула площади сферы S=4πR².    ⇒  S-4π•169=676•π см² или 2123,7 см²