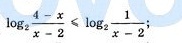Ответы
Ответ дал:
0
решение во вложении......................
Приложения:
Ответ дал:
0
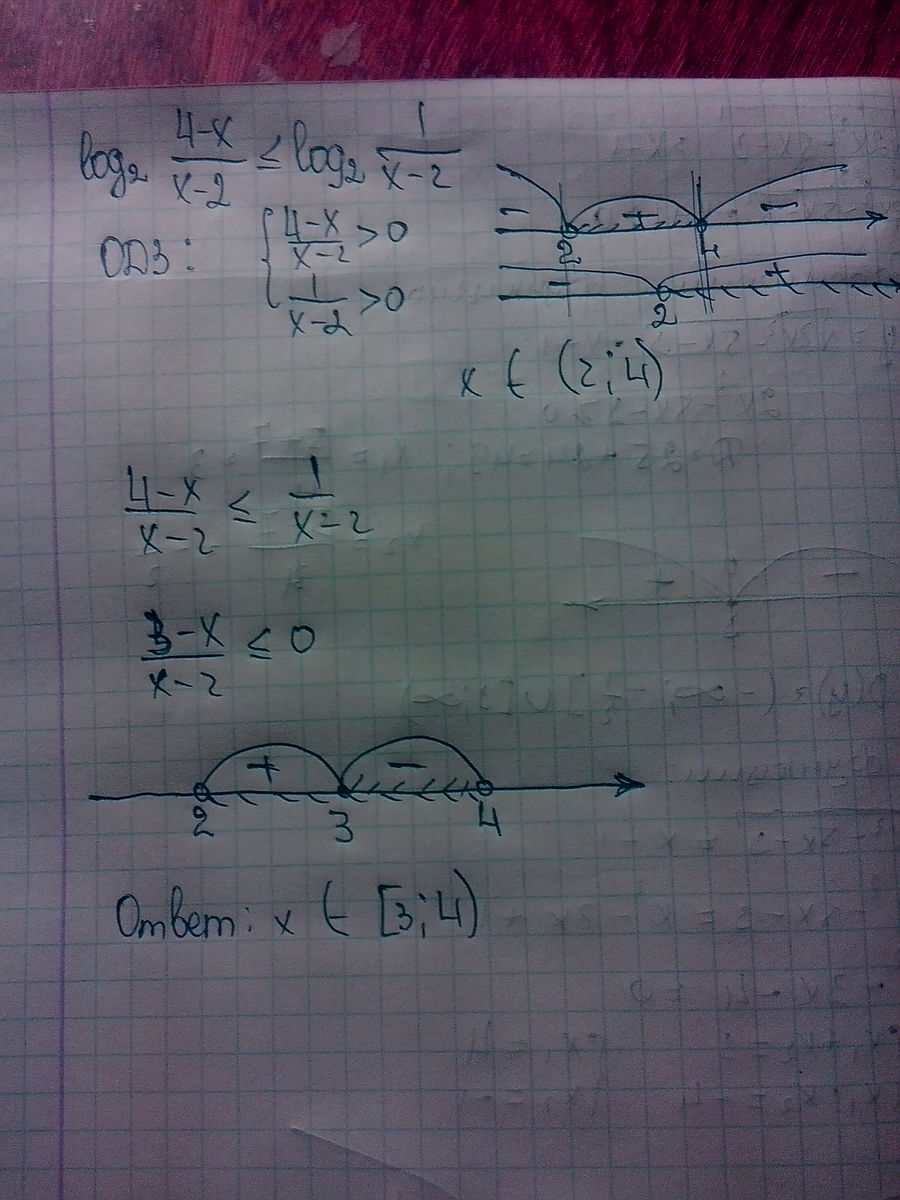
ОДЗ: 
Логарифмическая функция с основанием 2 - возрастает. Большему значению функции соответствует большее значение аргумента.

Учитывая, что

второе неравенство в нахождении ОДЗ
оказывается автоматически выполнено
Решаем первое неравенство

\\\\\\\\\ //////////////////////
-------------(2)-----------[3]-----------
Решаем первое неравенство

\\\\\\\\\\\\\\\
-------------(2)-----------------------(4)-------------
Пересечение двух ответов
[3;4)
Логарифмическая функция с основанием 2 - возрастает. Большему значению функции соответствует большее значение аргумента.
Учитывая, что
второе неравенство в нахождении ОДЗ
оказывается автоматически выполнено
Решаем первое неравенство
\\\\\\\\\ //////////////////////
-------------(2)-----------[3]-----------
Решаем первое неравенство
\\\\\\\\\\\\\\\
-------------(2)-----------------------(4)-------------
Пересечение двух ответов
[3;4)
Приложения:

Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад
10 лет назад