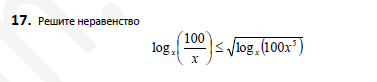Ответы
Ответ дал:
0
Рассмотрим функцию
Приравняем функцию к нулю
Упростим))
Пусть
Находим дискриминант
Возвращаемся к замене
полученное решение отметим на промежутке
(0)___-__
Ответ:
Вас заинтересует
2 года назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад