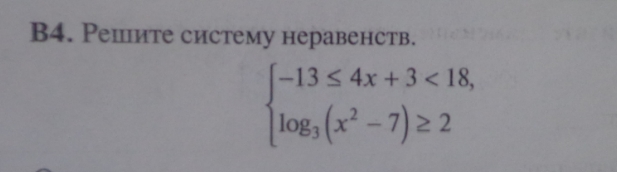Ответы
Ответ дал:
0
- 13 ≤ 4x +
3 ≤ 18
log₃ (x² - 7) ≥ 2
- 13 - 3 ≤ 4x ≤ 18 - 3
x² - 7 ≥ 3²
- 16 ≤ 4x ≤ 15
x² ≥ 9 + 7
1) - 4 ≤ x ≤ 3,75
x² ≥ 16
x₁ = - 4
x₂ = 4
+ - +
-------------------------------------------------------------->
- 4 4 x
2 ) x∈( - ≈; - 4] [4 ; + ≈)
Объединяя 1) и 2) получаем:
х∈ Ø
log₃ (x² - 7) ≥ 2
- 13 - 3 ≤ 4x ≤ 18 - 3
x² - 7 ≥ 3²
- 16 ≤ 4x ≤ 15
x² ≥ 9 + 7
1) - 4 ≤ x ≤ 3,75
x² ≥ 16
x₁ = - 4
x₂ = 4
+ - +
-------------------------------------------------------------->
- 4 4 x
2 ) x∈( - ≈; - 4] [4 ; + ≈)
Объединяя 1) и 2) получаем:
х∈ Ø
Вас заинтересует
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад