Помогите, пожалуйста, с производными!
Готова об стену биться, только эти два не получаются(
Приложения:
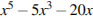
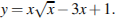
Ответы
Ответ дал:
0
На промежутке от -6 до -2 производная >0, ф-ция возрастает, от -2 до 1 убывает, наибольшее значение равно f(-2)=-32+5*8+40=48;
Критическая точка одна, x=4, смотрим на знаки производной по разные стороны, что доказывает, что x=4 - точка минимума
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад