Question

Даю 90 баллов за то, что задание действительно сложное. Помогите пожалуйста. Если можно по времени в пределах 1-2 часа. Решение сделать на листочке и фотографией. Если можно. Номер 20.

Answer 1

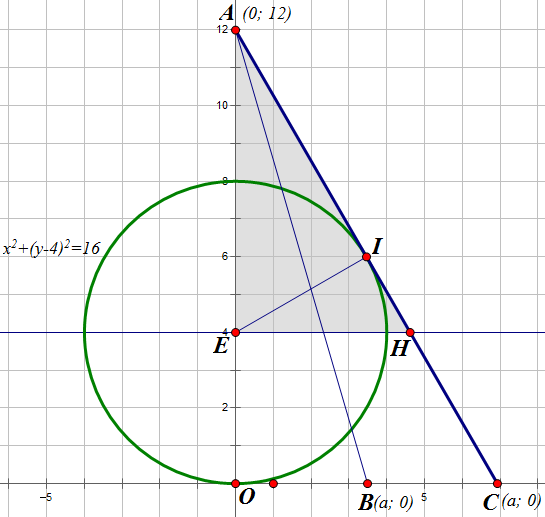
Наиболее эффективным в данном случае является геометрический метод решения. Первое уравнение задает на плоскости xOy окружность с центром в точке (0, 4) и радиусом 4 (выделена зеленым). Во втором уравнении в левой части стоит сумма расстояний от рассматриваемой точки (x; y) до точек A(0; 12) и B(a; 0). В правой части, как нетрудно заметить, формула расстояния между A и B. Для каких точек AM+MB=AB? Из неравенства треугольника следует, что все такие точки M лежат на прямой AB, и из очевидных соображений M лежит между A и B или совпадает с одной из них. Следовательно, второе уравнение задает некоторый отрезок, причем обе его граничные точки не лежат внутри окружности. Поскольку границы не внутри, конечность отрезка нам не важна, и прямая AB имеет с окружностью ровно одну точку пересечения, как и отрезок. Это возможно только если эта прямая является касательной.

Пусть при некотором a точка B попадает в точку C и AB касается окружности. Таких a два, но они равны по модулю, будем находить положительное. Рассмотрим прямоугольный треугольник AEH. AE=8; $EH=\frac23a=k$, так как он подобен △ABC, $AH=\sqrt{k^2+64}$, высота к гипотенузе EI равна 4, т.к. это радиус. Существует формула высоты к гипотенузе прямоугольного тр-ка, легко выводящаяся через площадь: $h=\frac{ab}{c}.$ Применим ее:
$4=\frac{k*8}{\sqrt{k^2+64}};\\ \sqrt{k^2+64}=2k;\\ k^2+64=4k^2;\\ k=\frac{8}{\sqrt3};\\ k=\frac23a ~\to~ a=4\sqrt3.$
Также не забываем про вторую касательную, симметричную первой.
Ответ: ±4√3.