Question

Помогите оооооооочень срочно
В равнобедренной трапеции диагональ перпендикулярна боковой стороне. Длина диагонали 12 см, проекция боковой стороны на большее основание-7 см. найдите большее основание и высоту трапеции.

Answer 1

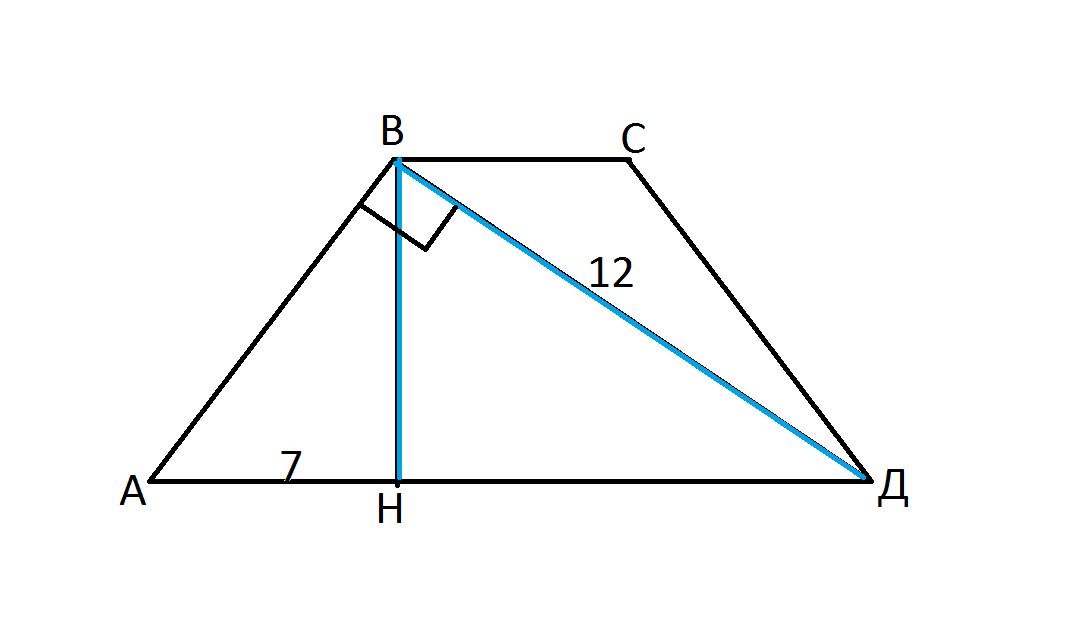
Трапеция АВСД. 
Угол АВД - прямой. 
Треугольник АВД - прямоугольный, АВ и ВД - катеты, АД - гипотенуза, ВН - высота этого треугольника и высота трапеции. 
Высота из прямого угла к гипотенузе делит ее на отрезки, которые являются проекциями катетов треугольника на гипотенузу. 

АН - проекция боковой стороны  АВ ( и катета треугольника АВС) на АД. 

Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы, заключенным между катетом и высотой. ⇒
                                ВД²=АД*ДН
Пусть ДН=х
Тогда АД=7+х
144=(7+х)*х ⇒
                               х²+7х-144=0
Решив квадратное уравнение, получим 
х₁=9
х₂=-16 ( не подходит)
НД=9
                              АД=7+9=16 см
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой:
ВН²=АН*НД
ВН²=7*9=63
                             ВН=√63=3√7 см..