Площадь треугольника ACE равна 90.На сторонах AC и CE треугольника взяты точки B и D таr что BD параллелен AE, BC:AC=1:3. Найдите площадь четырехугольника ABDE
Ответы
Ответ дал:
4
фото::::::::::::::::::::::::::::::::::::
Приложения:
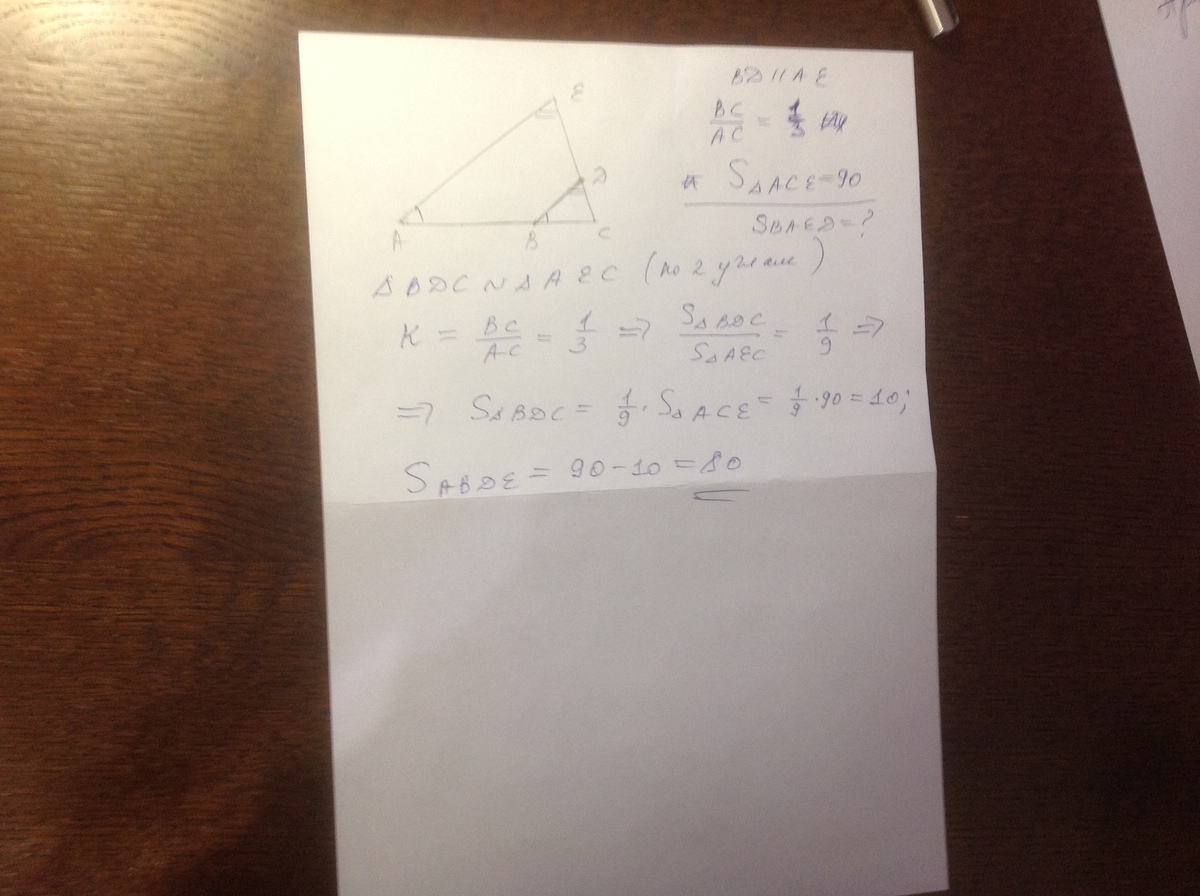
Nikolaymoiss:
Я не знаю как добавить на телефоне сюда фото
Ответ дал:
2
Так как BD параллельна AE. То все характеристики будут как 1 к 3. Следовательно и высота проведенная от точки С тоже будет относиться как 1 к 3. Следовательно по формуле  , где h - высота, a основание треугольника ACE площадь маленького треугольника будет равна
, где h - высота, a основание треугольника ACE площадь маленького треугольника будет равна  , где h1 и а1 те же параметры треугольника BCD. Т.к. h1 = 1/3h, а а1 = 1/3а, то по формуле
, где h1 и а1 те же параметры треугольника BCD. Т.к. h1 = 1/3h, а а1 = 1/3а, то по формуле  , т.е. в 9 раз меньше. Следовательно площадь треугольника BCD = 10, а площадь прямоугольника ABDE = 90-10 = 80
, т.е. в 9 раз меньше. Следовательно площадь треугольника BCD = 10, а площадь прямоугольника ABDE = 90-10 = 80
Вас заинтересует
2 года назад
7 лет назад
7 лет назад
9 лет назад