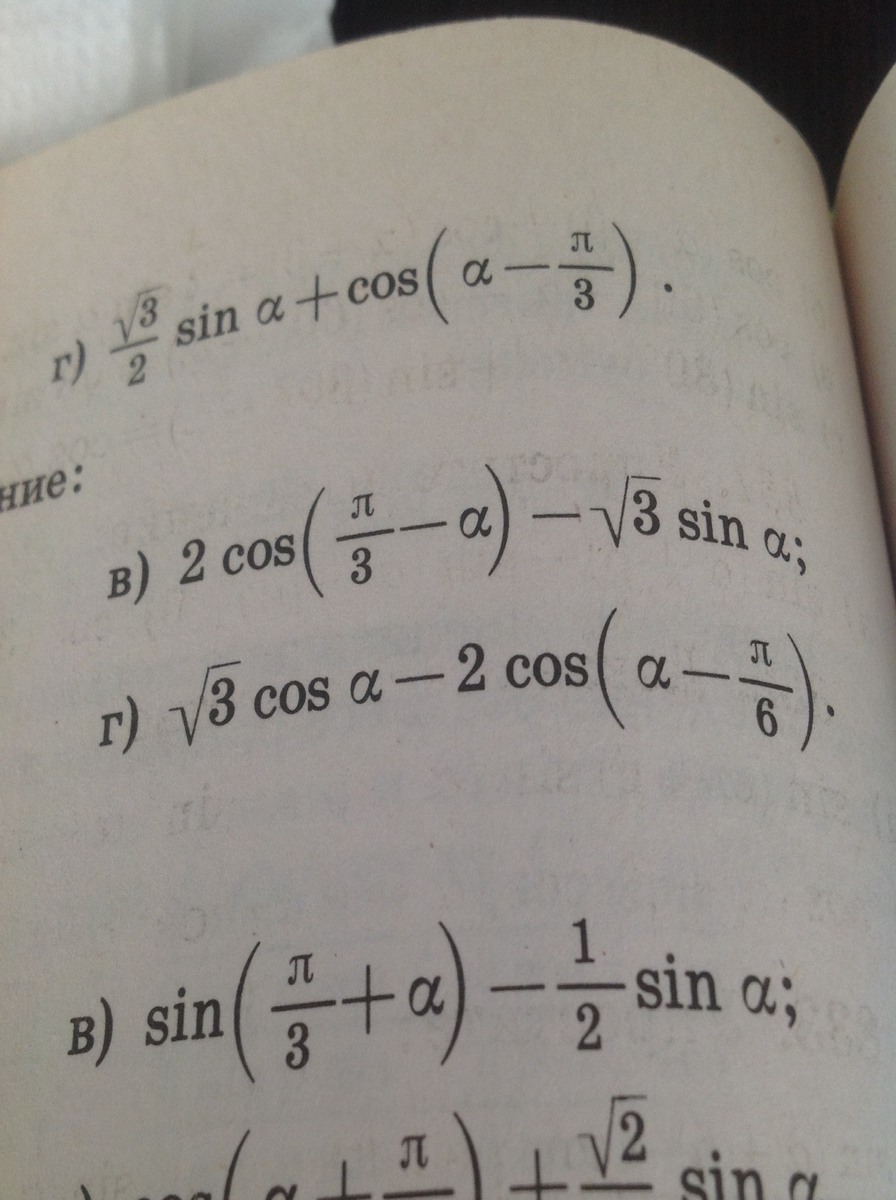Ответы
Ответ дал:
0
решение во вложении :)
Приложения:

Ответ дал:
0
Воспользуемся формулой 


Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад