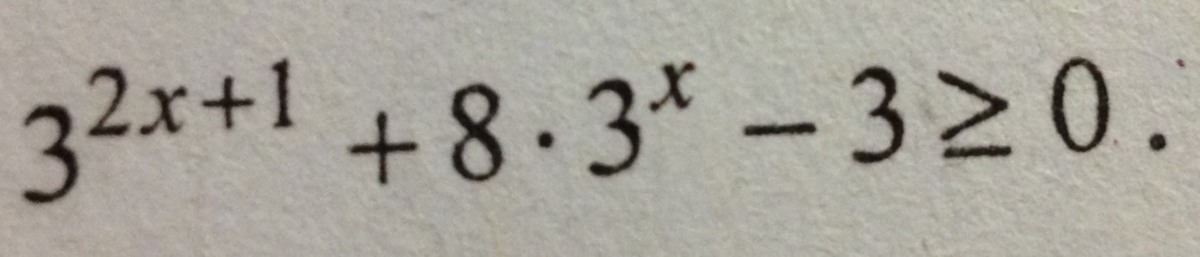Ответы
Ответ дал:
0
Ответ дал:
1
3^(2x)*3+8*3^x-3≥0
Обозначим 3^x=y, у>0
3y^2+8y-3=0
D=64+36=100
y₁=1/3
y₂=-3
3^x=1/3
x=-1
3^x=-3(посторонний корень)
Методом интервалов получим, что неравенство имеет решение при х∈[-1;+∞)
Решение неравенства х∈[-1;+∞)
Обозначим 3^x=y, у>0
3y^2+8y-3=0
D=64+36=100
y₁=1/3
y₂=-3
3^x=1/3
x=-1
3^x=-3(посторонний корень)
Методом интервалов получим, что неравенство имеет решение при х∈[-1;+∞)
Решение неравенства х∈[-1;+∞)
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад