Question

Расстояние от точки до плоскости равно 4см. Из этой точки проведены две наклонные, длина которых 5 см и 4√5 см. Угол между проекциями этих наклонных равен 60 градусов. Вычислите расстояние между основаниями этих наклонных. Приложите, пожалуйста, рисунок.

Answer 1

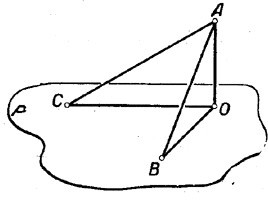
Расстояние от точки до плоскости АО=4см. Две наклонные АВ=5 см и АС=4√5 см. Угол ВОС между проекциями этих наклонных равен 60°. Найти  расстояние ВС между основаниями этих наклонных. Из прямоугольного ΔАВО:
ОВ=√(АВ²-АО²)=√(25-16)=√9=3
Из прямоугольного ΔАСО:
ОС=√(АС²-АО²)=√(80-16)=√64=8
Из ΔВОС по т.косинусов
ВС²=ОВ²+ОС²-2ОВ*ОС*cos 60=9+64-2*3*8*1/2=49
ВС=7