Планета, имеющая форму шара, делает один оборот вокруг своей оси за v=2,7⋅10^(-5) c. Если плотность планеты ρ=0,7⋅10^3кг/м^3, то вес тела на полюсе превышает вес на экваторе на ...(%)?
Ответы
Ответ дал:
0
Дано
Т=2,7*10^(-5) c период вращения планеты
ρ=0,7*10³ кг/м³ плотность вращения планеты
Натйти

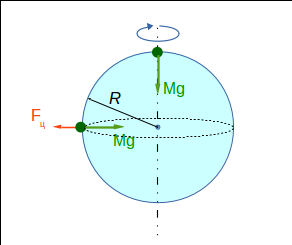
На полюсе вес равен силе тяжести
 (1)
(1)
На экваторе он меньше за счет центробежной силы.
 )
)
относительная разность весов:
 (3)
(3)
NB. Тут правда есть один условность. Что мы принимаем за 100%. Я принимал полярный вес, но можно было и иначе. Чтобы не возникало неоднозначности лучше было бы запросить отношения весов . Т.е спросить во сколько раз скажем полярный вес больше экваториального.
. Т.е спросить во сколько раз скажем полярный вес больше экваториального.
 (4
(4
При этом из закона всемирного тяготения и "геометрических соображений" выражаем g:
 (5)
(5)
Ускорение :
:
 (6)
(6)
Подставляем (5), (6) в (4)

 (6)
(6)
Вот только возникают сомнения насчет правильности данных о периоде вращения. Надо проверить вдруг ? В этом случае любое тело улетит с экватора. Тогда и пользоваться формулой (6) некорректно.
? В этом случае любое тело улетит с экватора. Тогда и пользоваться формулой (6) некорректно.
Проверим


Ну видно невооруженным глазом, что

При таком раскладе с экватора улетит все что можно, я подозреваю, что планету вообще разорвет в клочья( Если в природе вообще возможно такое ускорение)
Значит полагаем ошибка в условии и
T=2,7*10⁵ c
Тогда согласно (6):

Т=2,7*10^(-5) c период вращения планеты
ρ=0,7*10³ кг/м³ плотность вращения планеты
Натйти
На полюсе вес равен силе тяжести
На экваторе он меньше за счет центробежной силы.
относительная разность весов:
NB. Тут правда есть один условность. Что мы принимаем за 100%. Я принимал полярный вес, но можно было и иначе. Чтобы не возникало неоднозначности лучше было бы запросить отношения весов
При этом из закона всемирного тяготения и "геометрических соображений" выражаем g:
Ускорение
Подставляем (5), (6) в (4)
Вот только возникают сомнения насчет правильности данных о периоде вращения. Надо проверить вдруг
Проверим
Ну видно невооруженным глазом, что
При таком раскладе с экватора улетит все что можно, я подозреваю, что планету вообще разорвет в клочья( Если в природе вообще возможно такое ускорение)
Значит полагаем ошибка в условии и
T=2,7*10⁵ c
Тогда согласно (6):
Приложения:
Ответ дал:
0
Ну вот это по -моему больше похоже на правду.
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад