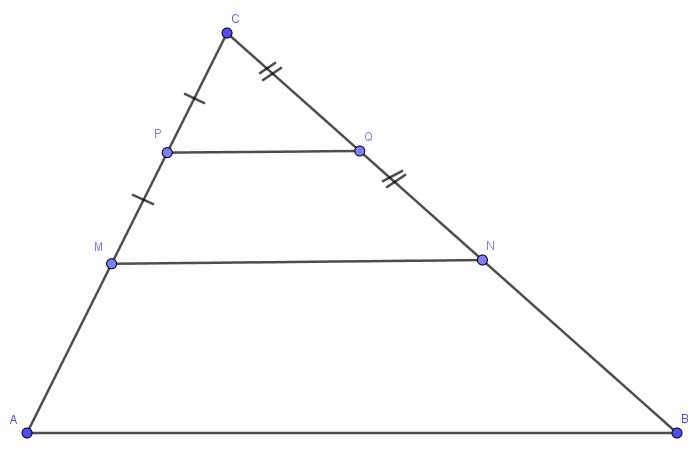
В треугольнике MNC,на сторонах NC и MC отмечены точки Q и P , так что NQ=QC и MP=PC. Найдите PQ, если AB=8, а MN-средняя линия треугольника ABC, параллельная AB
Ответы
Ответ дал:
0
Так как PQ — отрезок, соединяющий середины двух его сторон, то PQ - средняя линия треугольника MNC.
AB || MN и средняя линия треугольника равна половине параллельной стороне, т.е. MN = 1/2 * AB = 1/2 * 8 = 4
PQ || MN, аналогично PQ = 1/2 * MN = 1/2 * 4 = 2.
Ответ: 2.
Приложения:
Вас заинтересует
2 года назад
7 лет назад
10 лет назад
10 лет назад