Ответы
Ответ дал:
0
Дано:
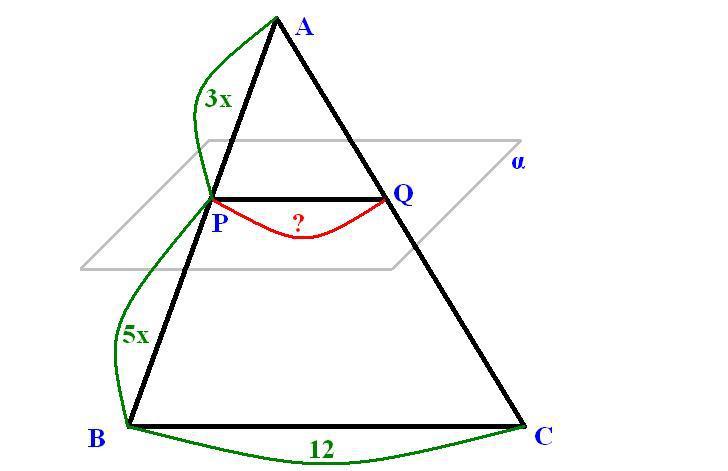
АВС - треугольник
α||BC, α∧АВ=Р, α∧АС=Q
AP/PB=3/5
BC=12 см
Найти: PQ
Решение:
Так как плоскость параллельна прямой ВС, то и любая прямая (в том числе РQ) параллельна прямой ВС. Так как РQ||ВС, то соответственные углы АPQ и АВС равны. Тогда треугольники АВС и АPQ подобны по двум углам (угол А - общий). Отношение сходственных сторон:

Ответ: 4,5 см
АВС - треугольник
α||BC, α∧АВ=Р, α∧АС=Q
AP/PB=3/5
BC=12 см
Найти: PQ
Решение:
Так как плоскость параллельна прямой ВС, то и любая прямая (в том числе РQ) параллельна прямой ВС. Так как РQ||ВС, то соответственные углы АPQ и АВС равны. Тогда треугольники АВС и АPQ подобны по двум углам (угол А - общий). Отношение сходственных сторон:
Ответ: 4,5 см
Приложения:
Вас заинтересует
2 года назад
10 лет назад
10 лет назад
10 лет назад
10 лет назад
