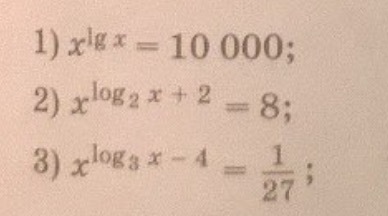Ответы
Ответ дал:
0
1) 
ОДЗ:




 или
или 
 или
или 
 или
или 
Ответ:

2)
ОДЗ:



Замена:




 или
или 
 или
или 
Ответ:

3)
ОДЗ:




Замена:




 или
или 
 или
или 
Ответ:

ОДЗ:
Ответ:
2)
ОДЗ:
Замена:
Ответ:
3)
ОДЗ:
Замена:
Ответ:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад