Question

ДОкажите,что если четыре прямые, проходящие через точку А, пересекают плоскость альфа в вершинах параллелограмма,то они пересекают любую плоскость ,параллельную плоскости альфа и не проходящие через точку А,тоже в вершинах параллелограмма

Answer 1

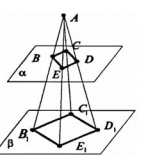
Пусть А — данная точка, ВСDЕ — данный параллелограмм.

Рассмотрим плоскости BAC, CAD, DAE, EAB.

 

По теореме о пересечении двух параллельных плоскостей третьей:

BC||B1C1, CD||C1D1, ED||E1D1, BE||B1E1.

Так что B1C1||BC||ED||E1D1, то есть B1C1||E1D1 и B1E1||BE||CD||C1D1 то есть B1E1||C1D1.

Значит B1C1D1E1 —  параллелограмм