Ответы
Ответ дал:
0
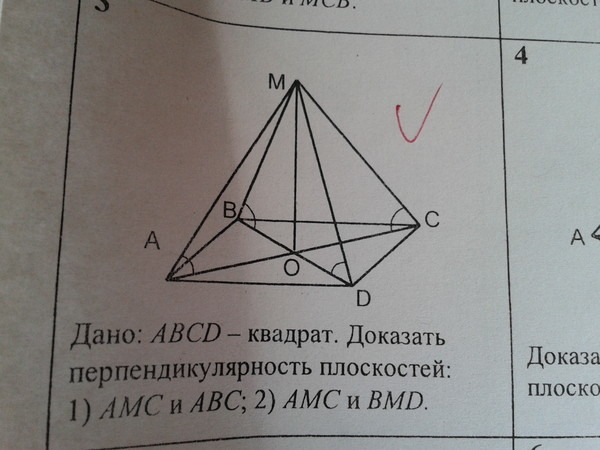
Высота пирамиды MO.
∠MAO =∠MBO=∠MCO =∠MDO( отмечены на рисунке) , поэтому и
∠AMO =∠BMO=∠CMO =∠DMO ,значить
ΔMAO=ΔMBO=ΔMCO=ΔMDO.
Следовательно точка O есть центр окружности описанной около основания ,т.е. пересечения диагоналей AC и BD, притом AC⊥ BD_свойство квадрата.
(AMC) ⊥ (ABCD)
* * *Плоскость AMC проходит через прямой MO, которая перпендикулярна плоскости ABCD * * *
(AMC) ⊥ (ABCD) ⇔(AMC) ⊥ (ABC) .
---
Плоскость AMC перпендикулярна плоскости BMD, т.к.
плоскость AMC проходит через прямую AC ,которая ⊥ (BMD).
Действительно MO ⊥ AС ⇔AС ⊥ MO и еще AС⊥ BD ⇒AC ⊥ (BMD) .
∠MAO =∠MBO=∠MCO =∠MDO( отмечены на рисунке) , поэтому и
∠AMO =∠BMO=∠CMO =∠DMO ,значить
ΔMAO=ΔMBO=ΔMCO=ΔMDO.
Следовательно точка O есть центр окружности описанной около основания ,т.е. пересечения диагоналей AC и BD, притом AC⊥ BD_свойство квадрата.
(AMC) ⊥ (ABCD)
* * *Плоскость AMC проходит через прямой MO, которая перпендикулярна плоскости ABCD * * *
(AMC) ⊥ (ABCD) ⇔(AMC) ⊥ (ABC) .
---
Плоскость AMC перпендикулярна плоскости BMD, т.к.
плоскость AMC проходит через прямую AC ,которая ⊥ (BMD).
Действительно MO ⊥ AС ⇔AС ⊥ MO и еще AС⊥ BD ⇒AC ⊥ (BMD) .
Ответ дал:
0
Спасибо большое!)
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад