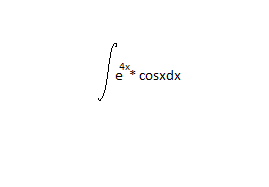Ответы
Ответ дал:
0
Надо интегрировать два раза частями, чтоб получить в правой части тот же интеграл, что в начале + функцию
Интегрируем 1 раз
u - e^(4x)
dv - cosx
e^(4x)*cosx dx= [v=sinx]=e^(4x)*sinx-sinx d(e^(4x))===
Интегрируем 2 раз
sinx d(e^(4x))=4sinx e^(4x)dx= [v=-cosx]=4(-e^(4x)cosx + cosxd(e^(4x)))=
u - e^(4x)
dv - sinx
=4(-e^(4x)cosx +4cosx e^(4x) dx)
===e^(4x)*sinx+ 4e^(4x)cosx - 16cosx e^(4x) dx
имеем
e^(4x)*cosx dx = e^(4x)*sinx+4e^(4x)cosx- 16cosx e^(4x) dx
или
17e^(4x)*cosx dx=e^(4x)*sinx+4e^(4x)cosx
e^(4x)*cosx dx=(e^(4x)*sinx+4e^(4x)cosx)/17+C
Интегрируем 1 раз
u - e^(4x)
dv - cosx
e^(4x)*cosx dx= [v=sinx]=e^(4x)*sinx-sinx d(e^(4x))===
Интегрируем 2 раз
sinx d(e^(4x))=4sinx e^(4x)dx= [v=-cosx]=4(-e^(4x)cosx + cosxd(e^(4x)))=
u - e^(4x)
dv - sinx
=4(-e^(4x)cosx +4cosx e^(4x) dx)
===e^(4x)*sinx+ 4e^(4x)cosx - 16cosx e^(4x) dx
имеем
e^(4x)*cosx dx = e^(4x)*sinx+4e^(4x)cosx- 16cosx e^(4x) dx
или
17e^(4x)*cosx dx=e^(4x)*sinx+4e^(4x)cosx
e^(4x)*cosx dx=(e^(4x)*sinx+4e^(4x)cosx)/17+C
Ответ дал:
0
А === это что обозначает
Ответ дал:
0
не знаю правильно ли, но идея - ето точняк
Ответ дал:
0
Спасибо братан
Ответ дал:
0
=== их два, ето =, просто между ними надо было зделать промежуточные вычисления (найти интеграл). вообщем ето =
Ответ дал:
0
незачто
Вас заинтересует
2 года назад
7 лет назад
10 лет назад