В равнобедренном треугольнике ABC с основанием BC проведены высоты BD и CE . Докажите , что прямые BC и DE параллельны .
Ответы
Ответ дал:
0
если что не понятно, пиши, объясню
Приложения:
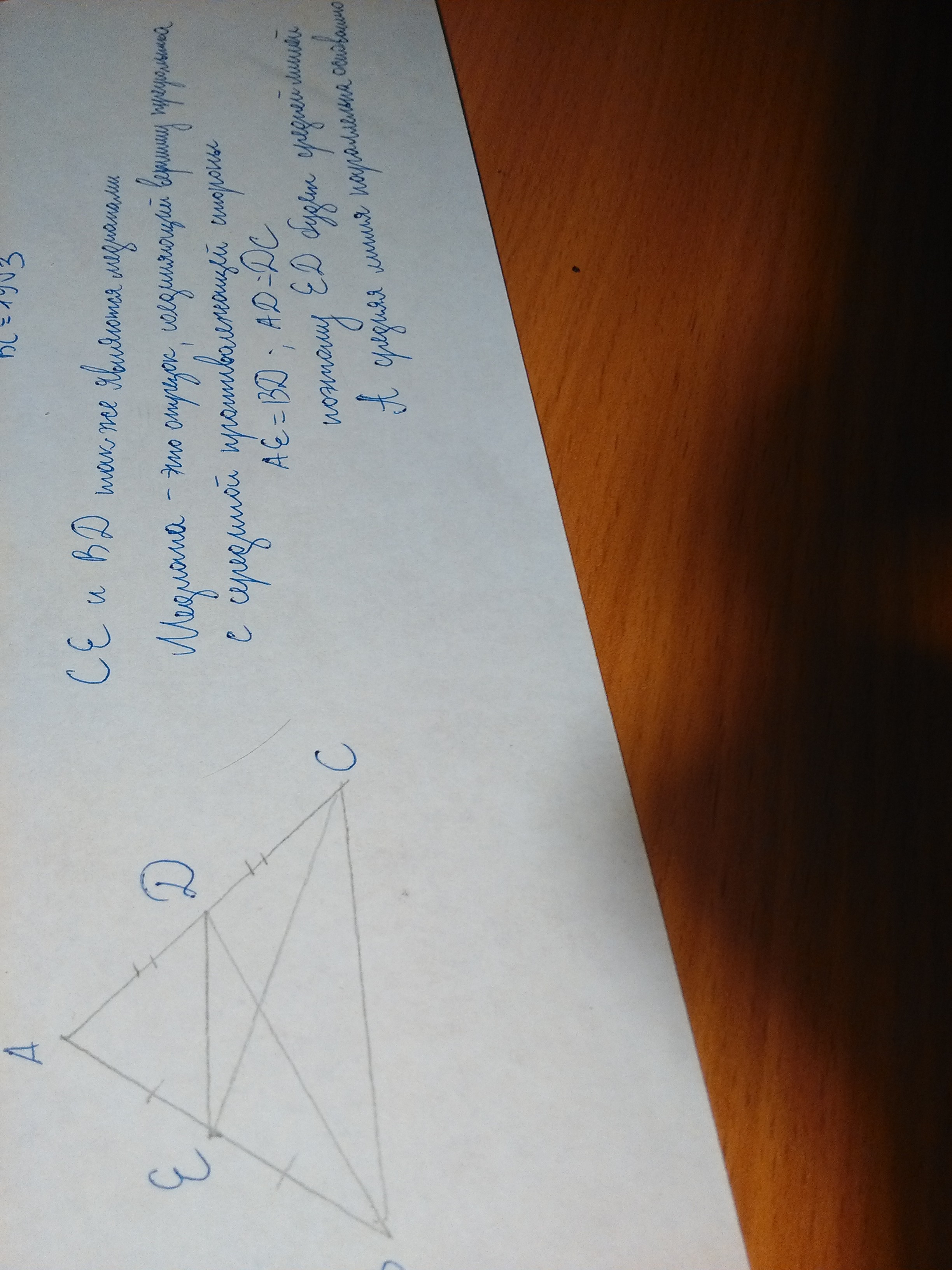
Ответ дал:
0
СЕ и ВД не являются медианами в равнобедренном треугольнике, только в правильном. Не надо путать.
Ответ дал:
0
Опустим высоты ЕМ и ДК на основание ВС.
Треугольники ВСД и СВЕ равны (∠ВСД=∠СВЕ, оба прямоугольные,сторона ВС общая), значит ЕМ=ДК.
МЕДК - прямоугольник, в нём ДЕ║МК, значит ДЕ║ВС.
Доказано.
Треугольники ВСД и СВЕ равны (∠ВСД=∠СВЕ, оба прямоугольные,сторона ВС общая), значит ЕМ=ДК.
МЕДК - прямоугольник, в нём ДЕ║МК, значит ДЕ║ВС.
Доказано.
Приложения:
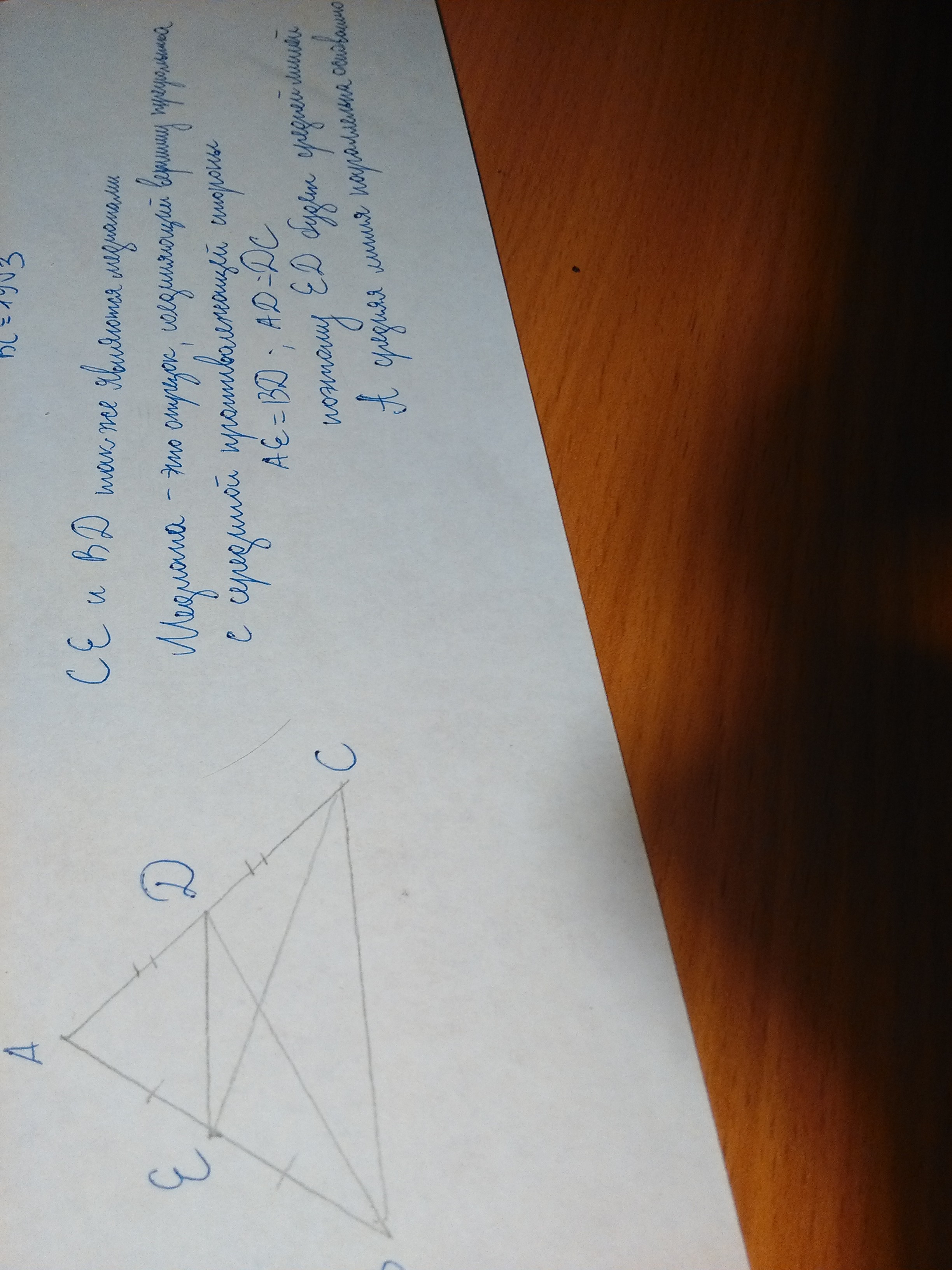
Ответ дал:
0
Извини , а откуда ты взял высоты EM и DK
Ответ дал:
0
чтобы решить задачу нужно сделать дополнительные построения. Опуская высоты ЕМ и ДК мы получаем четырёхугольник МЕДК, доказываем, что он прямоугольник, а у прямоугольника противоположные стороны равны. Всё, задача решена.
Вас заинтересует
2 года назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад