Ответы
Ответ дал:
0
Применены: способ подстановки, правила действий с алгебраическими дробями
Приложения:
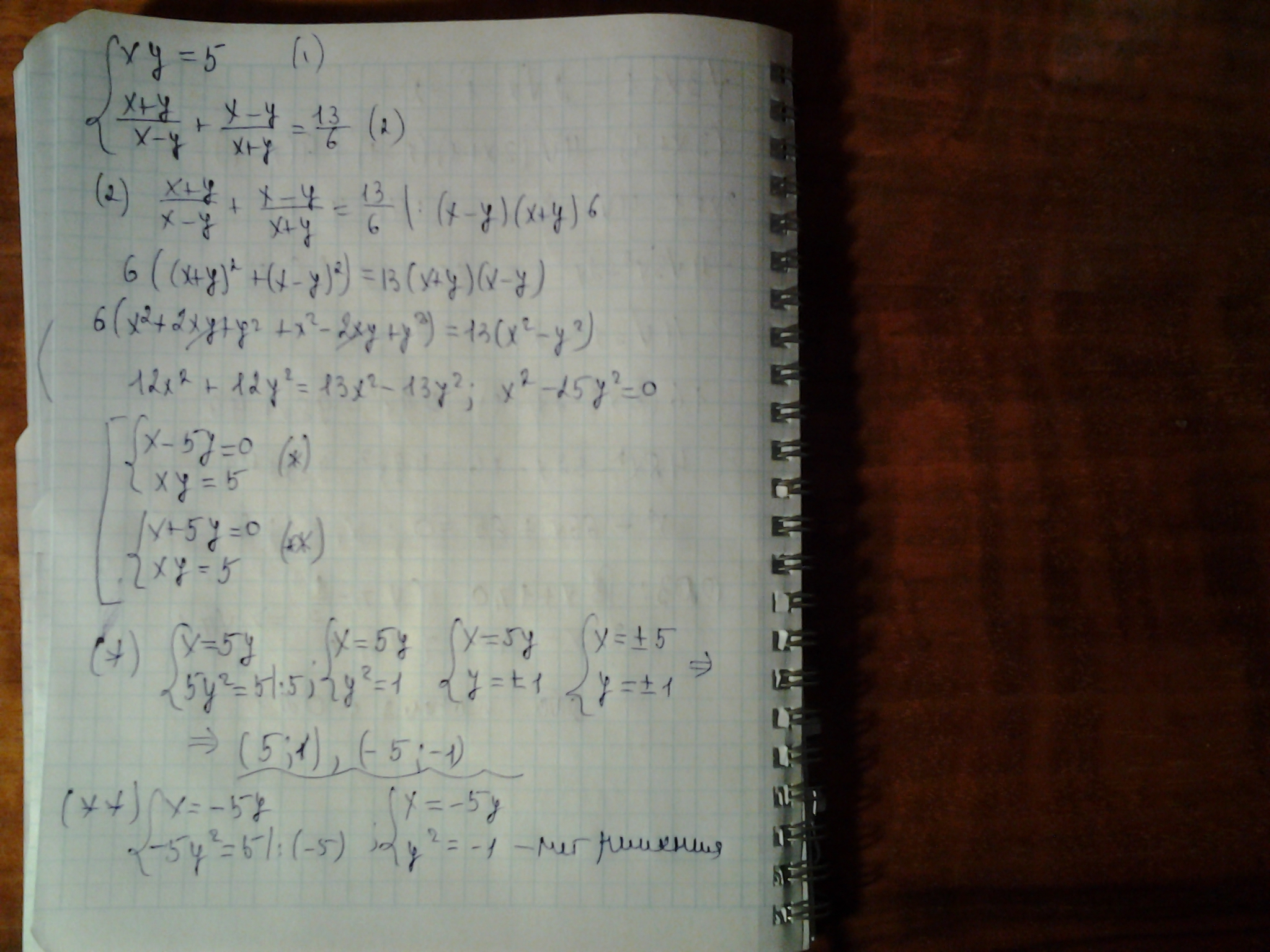
Ответ дал:
0
Ваше решение не совсем корректно, потому что вы не проверяете знаменатели на равенство нулю. Если один из Ваших знаменателей равен нулю, то при умножении на него то будет грубой ошибкой.
Ответ дал:
0
Если хоть один из знаменателей равен 0, то система изначально не корректна. А вот полученные корни были найдены из утверждения, что знаменатели не равны 0, когда я умножала на них
Ответ дал:
0
Да! Искреннее спасибо за внимание)
Ответ дал:
0
По второму уравнению видим, что один из множителей должен быть равен 0, то есть либо
Значит y = 1 или -1.
А во втором случае, аналогично, получим, что
Значит y = 1 или -1. Осталось найти x. Его мы можем найти по формуле
Приложения:
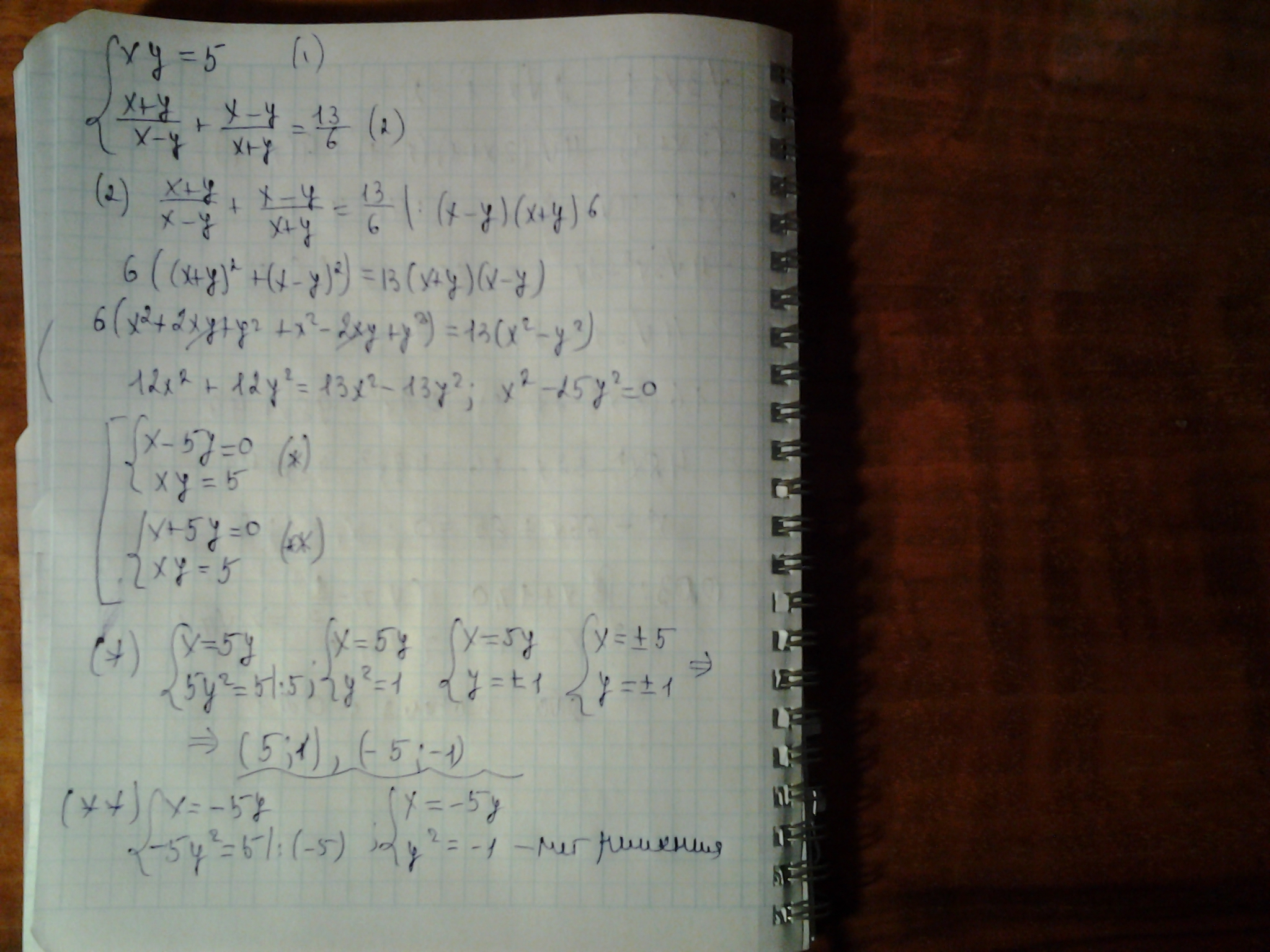
Вас заинтересует
2 года назад
7 лет назад
10 лет назад