Основание AC равнобедренного треугольника ABC равно 12.
Окружность радиуса 8 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине.
Найдите радиус окружности, вписанной в треугольник ABC.
Ответы
Ответ дал:
0
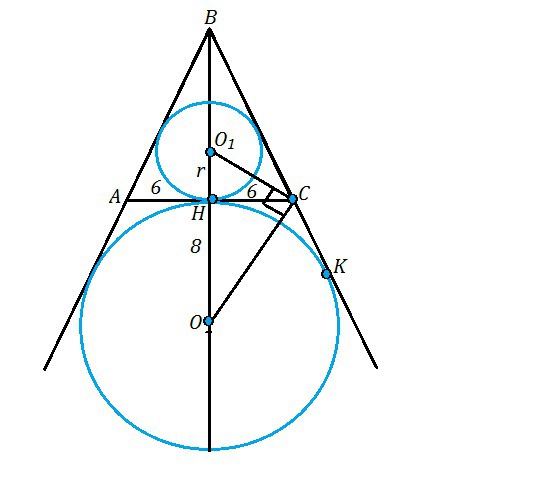
Центр вписанной в угол окружности лежит на его биссектрисе. Окружность радиуса 8 - вневписанная, касается сторон двух углов - А и С, ее центр лежит на пересечении биссектрис этих углов, смежных с углами А и С ∆ АВС соответственно,⇒
СО - биссектриса и делит угол НСК пополам. .
Центр окружности, вписанной в треугольник АВС, лежит в точке пересечения биссектрис. ВН и СО₁- биссектрисы.
СО₁ делит угол ВСН пополам.
АСК - развернутый угол и равен 180º
Сумма половин углов АСН и ОСН равна половине развернутого угла.
Угол ОСО₁=180°:2=90°⇒
∆ ОСО₁ - прямоугольный с прямым углом С.
АН - высота и медиана равнобедренного треугольника АВС, следовательно, делит основание АС на два равных отрезка:
СН=АН=6.
СН ⊥ АН⇒ является высотой треугольника ОСО₁.
СО - биссектриса и делит угол НСК пополам. .
Центр окружности, вписанной в треугольник АВС, лежит в точке пересечения биссектрис. ВН и СО₁- биссектрисы.
СО₁ делит угол ВСН пополам.
АСК - развернутый угол и равен 180º
Сумма половин углов АСН и ОСН равна половине развернутого угла.
Угол ОСО₁=180°:2=90°⇒
∆ ОСО₁ - прямоугольный с прямым углом С.
АН - высота и медиана равнобедренного треугольника АВС, следовательно, делит основание АС на два равных отрезка:
СН=АН=6.
СН ⊥ АН⇒ является высотой треугольника ОСО₁.
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой;⇒
СН²=ОН•HO₁
36=8 HO₁
HO₁=36/8=4,5 (ед. длины)
Приложения:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад