В правильной четырехугольной призме ABCDA1B1C1D1 все рёбра равны 4. На ребре AA1 взята точка M так, что AM=1. На ребре BB1 взята точка K так, что B1K=1. Найдите угол между плоскостью D1MK и плоскостью CC1D1
Ответы
Ответ дал:
0
решение в скане..................
Приложения:

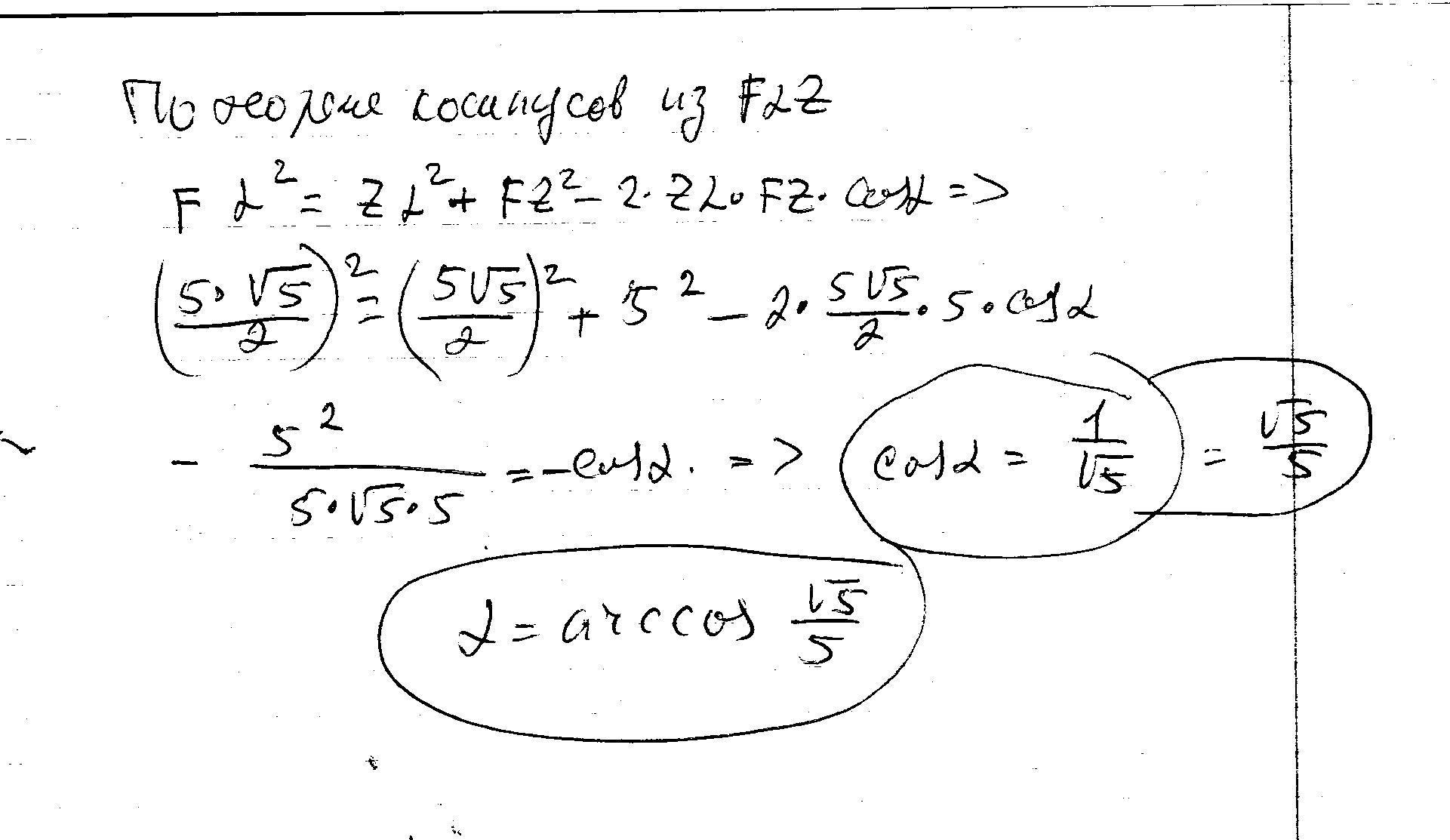
Ответ дал:
0
нет, это неверно. Она - параллелограмм
Ответ дал:
0
ВОт здесь, вероятно. Но перпендикулярность FZ nfv b yt ye;yf
Ответ дал:
0
там и не нужна. Все, кажется уже нет сил. РПойду спать. Спасибо, уже можно определиться где искать.
Ответ дал:
0
Нужна. А как вы тогда будете ситать угол между плоскостями?
Ответ дал:
0
ну, ладно
Ответ дал:
0
Пусть A - начало координат, а оси х, у, z пустим вдоль векторов AD, AB, AA₁ соответственно.
Вектор AD=(4,0,0) - перпендикулярен к плоскости CC₁D₁.
Плоскость D₁MK параллельна векторам
MD₁=(4,0,3) и MK=(0,4,2), значит векторное произведение
n=MD₁×MK=(-12,-8,16) перпендикулярно плоскости D₁MK.
Косинус угла между плоскостями CC₁D₁ и D₁MK равен
cos(AD,n)=(AD,n)/(|AD|·|n|)=-12·4/(4·4√(9+4+16))=-3/√29.
Значит острый угол между плоскостями равен arccos(3/√29).
Вектор AD=(4,0,0) - перпендикулярен к плоскости CC₁D₁.
Плоскость D₁MK параллельна векторам
MD₁=(4,0,3) и MK=(0,4,2), значит векторное произведение
n=MD₁×MK=(-12,-8,16) перпендикулярно плоскости D₁MK.
Косинус угла между плоскостями CC₁D₁ и D₁MK равен
cos(AD,n)=(AD,n)/(|AD|·|n|)=-12·4/(4·4√(9+4+16))=-3/√29.
Значит острый угол между плоскостями равен arccos(3/√29).
Приложения:

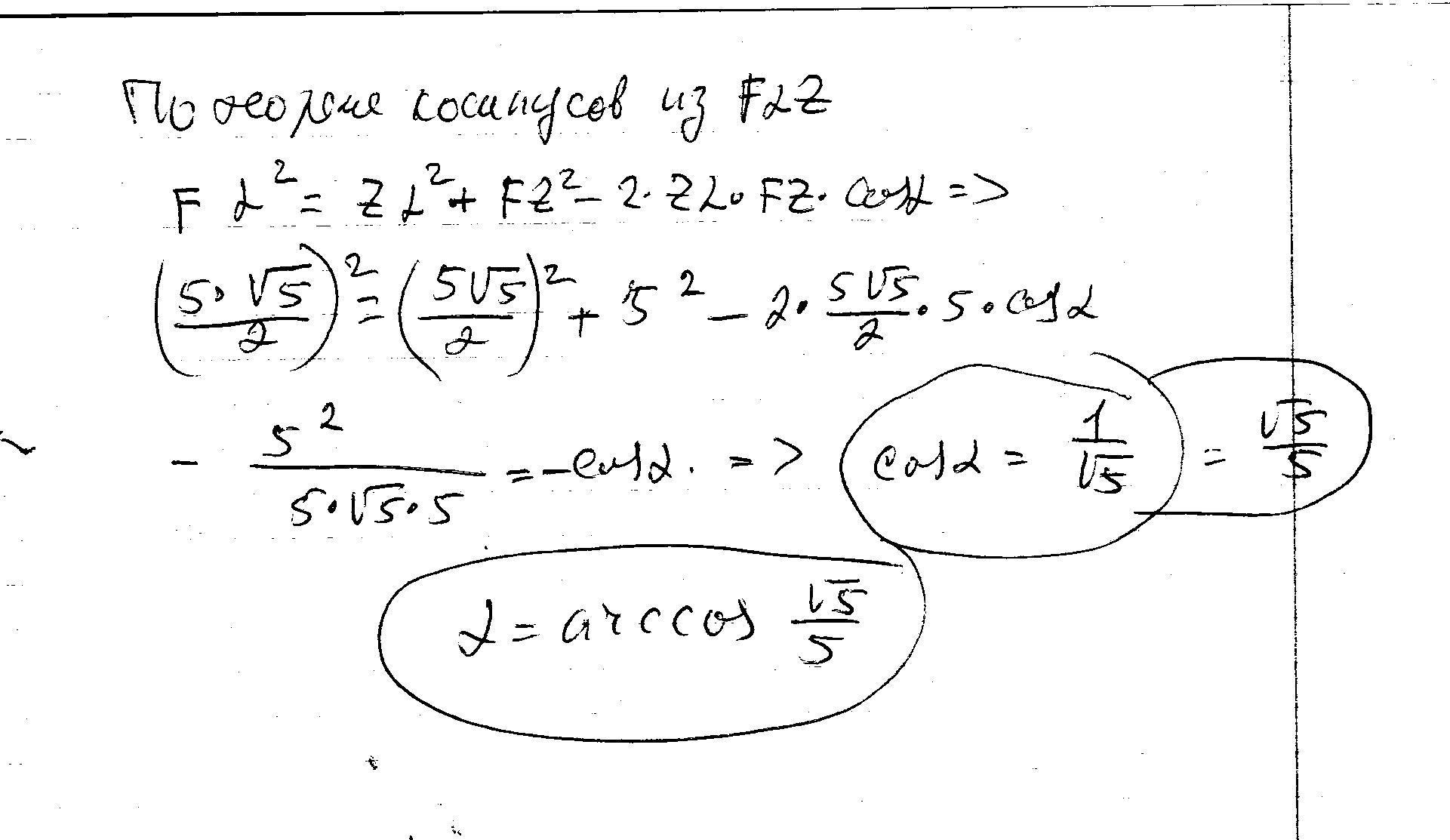
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад