Question

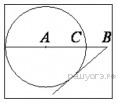
На отрезке AB выбрана точка C так, что AC=60 и BC=1 . Построена окружность с центром A , проходящая через C . Найдите длину отрезка касательной, проведённой из точки B к этой окружности.

Answer 1

Пусть точка пересечения касательной и окружности = N. Треугольник АNВ- прямоугольный ( Свойство касательной к окружности , проведённой из данной точки , лежащей вне окружности ) , причём угол N=90°.
Катет АN=R=60 , гипотенуза АВ=АС+СВ=60+1=61
По теореме Пифагора :
ВN²=АВ²-АN²     
ВN²=61²-60²=3721-3600=121
ВN=√121=11
Ответ: 11