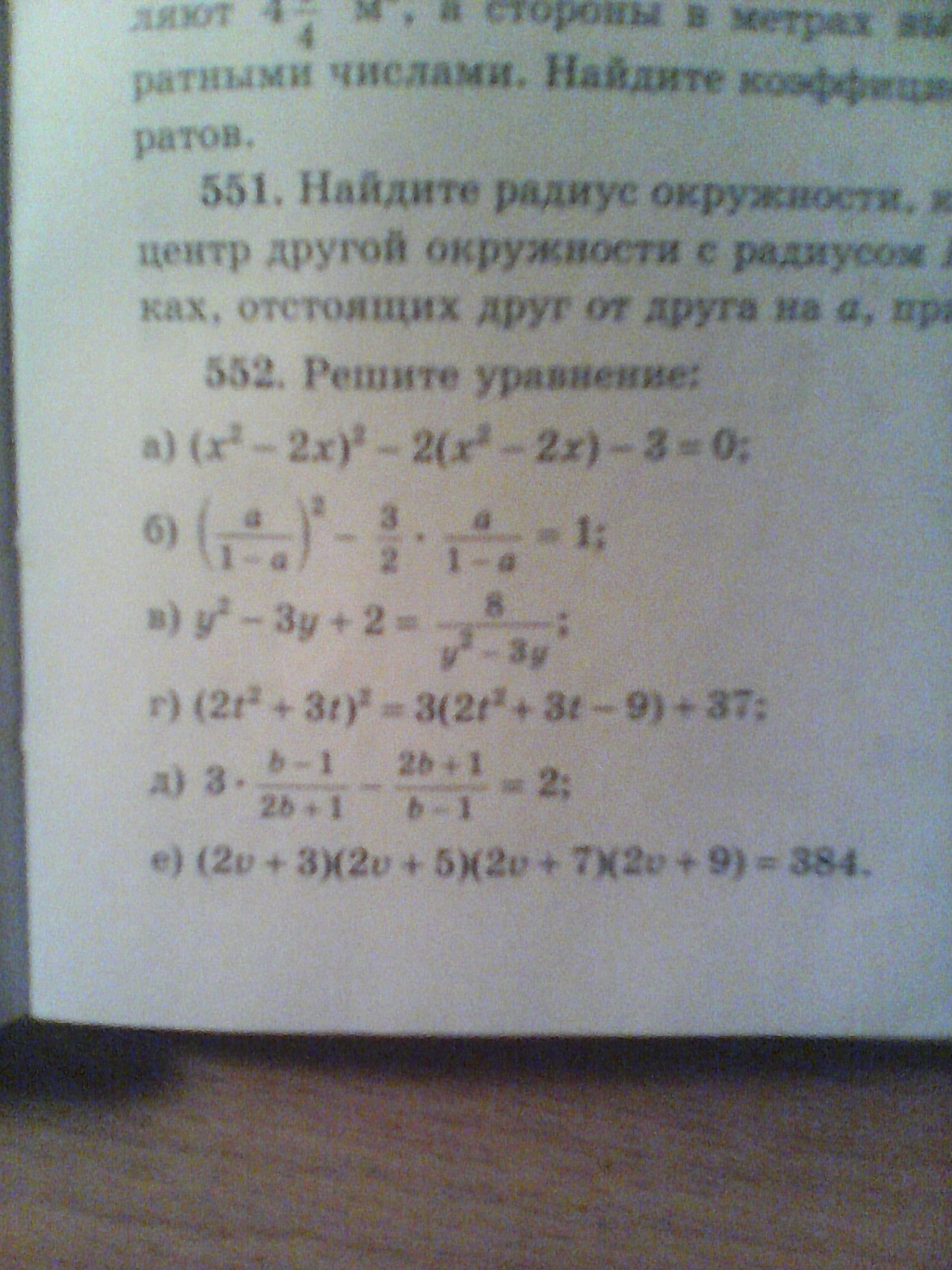Ответы
Ответ дал:
0
Решить уравнение:

Решение:
Сделаем замену. Пусть , тогда будем иметь:
, тогда будем иметь:

Получили квадратное уравнение. Найдем дискриминант квадратного уравнения:

 , значит квадратное уравнение имеет 2 корня., найдем эти корни:
, значит квадратное уравнение имеет 2 корня., найдем эти корни:

Обратная замена:

Аналогично, с предыдущим квадратным уравнением будем иметь:

 , квадратное уравнение имеет 2 корня:
, квадратное уравнение имеет 2 корня:


Найдем дискриминант квадратного уравнения

 , значит квадратное уравнение действительных корней не имеет.
, значит квадратное уравнение действительных корней не имеет.
Окончательный ответ:
Решение:
Сделаем замену. Пусть
Получили квадратное уравнение. Найдем дискриминант квадратного уравнения:
Обратная замена:
Аналогично, с предыдущим квадратным уравнением будем иметь:
Найдем дискриминант квадратного уравнения
Окончательный ответ:
Вас заинтересует
2 года назад
10 лет назад