Question

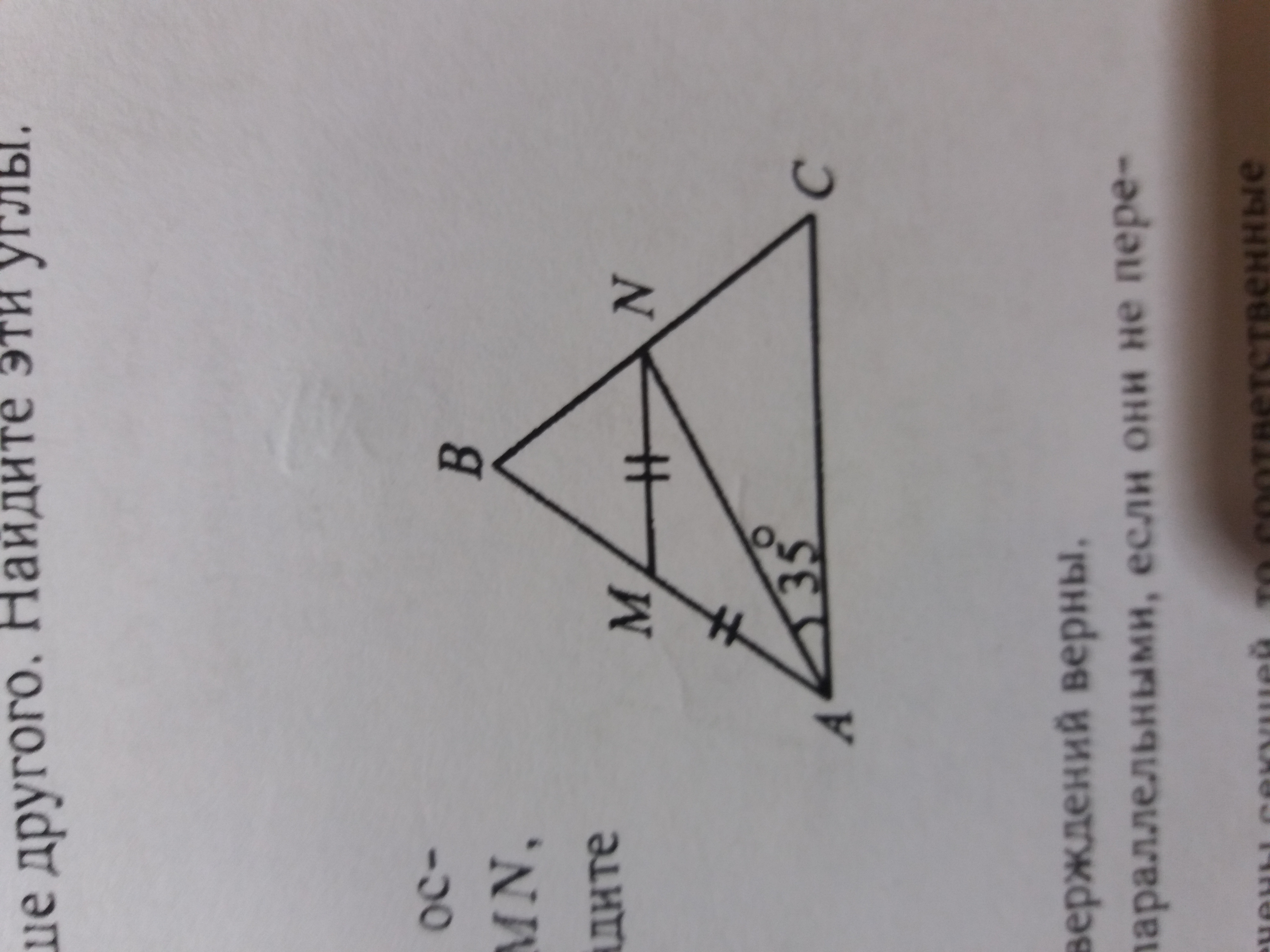
В равнобедренном треугольнике АВС с основанием АС угол С равен 70°, АМ= МN, угол CAN=35°. Докажите, что МN || АС. Найдите угол BMN.

Answer 1

Ответ:

1) Доказано, что MN || AC;    2) ∠BMN = 70°

Объяснение:

В треугольнике АВС  ∠А = ∠С = 70°, как углы при основании АС равнобедренного  треугольника

∠MAN = ∠A - ∠CAN = 70° - 35° = 35°

Δ AMN равнобедренный  так как по условию АМ = МN.

Значит, ∠ANM = ∠MAN = 35°

∠ANM = ∠CAN, это накрест лежащие углы при прямых MN и AC и секущей AN. Следовательно, MN || AC, что и требовалось доказать.

∠BMN = ∠A = 70°  как соответственные углы при  MN || AC и секущей АМ.