Question

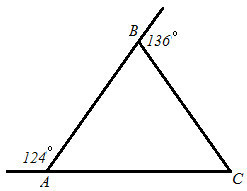
. Используя рисунок, выберите верные утверждения:
а) △ABC – равнобедренный;
б) △ABC – тупоугольный;
в) ∠C=80°
г) ∠2 – внешний для △ABC.

Answer 1

Найдем все углы ΔАВС.
Внешний угол при вершине В  смежный с ∠АВС . Следовательно :
∠АВС =180 - 136 = 44°
Внешний угол при вершине А смежный с ∠ВАС . Следовательно:
∠ВАС =180 - 124 = 56°   
Сумма углов любого треугольника  = 180°.
∠ВСА =180  - (44+56) = 80°

а)  Утверждение неверное.
В равнобедренном треугольнике углы при основании равны.
В Δ АВС  равных  углов нет. ⇒ΔАВС не является  равнобедренным.

б) Утверждение неверное.
Тупоугольный треугольник  - треугольник, содержащий тупой угол,
т.е.  один из его углов должен быть больше 90 °.
 В ΔАВС  таких  углов  нет.  ⇒   ΔАВС не является тупоугольным.

в) Утверждение верное.
∠С = ∠ВСА = 80°    

с)Т.к. ∠2 на чертеже не отмечен, то проверить данное утверждение невозможно.

Answer 2

пасиб большое