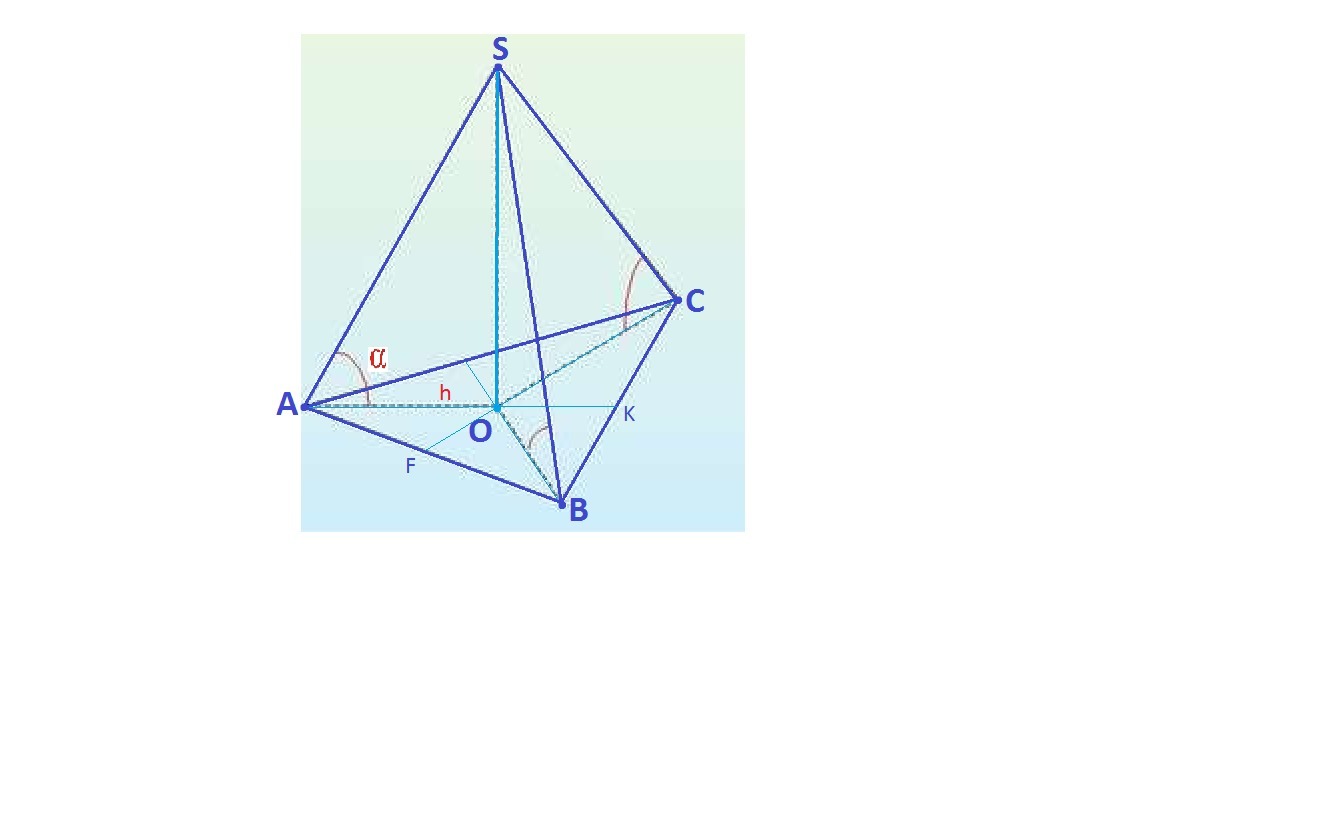
в правильной треугольной пирамиде высота основания равна h боковые ребра наклонены к основанию под углом Альфа. найдите объем пирамиды. с рисунком пожалуйста
Ответы
Ответ дал:
0
Δ
Δ
Δ
По теореме Пифагора:
Ответ:
Приложения:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
10 лет назад