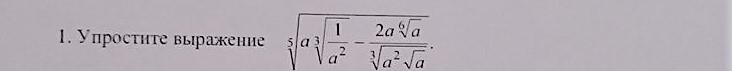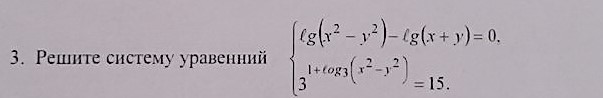Ответы
Ответ дал:
0
1
![sqrt[5]{asqrt[3]{dfrac1{a^2}}-dfrac{2asqrt[6]a}{sqrt[3]{a^2sqrt a}}}=sqrt[5]{a^{1-2/3}-2a^{1+1/6-(2+1/2)/3}}=\=sqrt[5]{a^{1/3}-2a^{1/3}}=sqrt[5]{-a^{1/3}}=-sqrt[15]a sqrt[5]{asqrt[3]{dfrac1{a^2}}-dfrac{2asqrt[6]a}{sqrt[3]{a^2sqrt a}}}=sqrt[5]{a^{1-2/3}-2a^{1+1/6-(2+1/2)/3}}=\=sqrt[5]{a^{1/3}-2a^{1/3}}=sqrt[5]{-a^{1/3}}=-sqrt[15]a](https://tex.z-dn.net/?f=sqrt%5B5%5D%7Basqrt%5B3%5D%7Bdfrac1%7Ba%5E2%7D%7D-dfrac%7B2asqrt%5B6%5Da%7D%7Bsqrt%5B3%5D%7Ba%5E2sqrt+a%7D%7D%7D%3Dsqrt%5B5%5D%7Ba%5E%7B1-2%2F3%7D-2a%5E%7B1%2B1%2F6-%282%2B1%2F2%29%2F3%7D%7D%3D%5C%3Dsqrt%5B5%5D%7Ba%5E%7B1%2F3%7D-2a%5E%7B1%2F3%7D%7D%3Dsqrt%5B5%5D%7B-a%5E%7B1%2F3%7D%7D%3D-sqrt%5B15%5Da)
2 Начнем со второго уравнения. Чтобы логарифм существовал, должно выполняться x^2 - y^2 > 0. Упрощаем:

Замечаем, что о выполнении неравенства можно не беспокоиться, 5 > 0, подставляем в первое:

Тогда
Получили систему:

Мой любимый способ решать такие системы - сложить и вычесть уравнения, получится 2x = 6 и 2y = 4, откуда x = 3 и y = 2.
Ответ: (3, 2).
2 Начнем со второго уравнения. Чтобы логарифм существовал, должно выполняться x^2 - y^2 > 0. Упрощаем:
Замечаем, что о выполнении неравенства можно не беспокоиться, 5 > 0, подставляем в первое:
Тогда
Получили систему:
Мой любимый способ решать такие системы - сложить и вычесть уравнения, получится 2x = 6 и 2y = 4, откуда x = 3 и y = 2.
Ответ: (3, 2).
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад