Ответы
Ответ дал:
0
Находим производную функции.
Приравниваем производную к нулю, чтобы найти критические точки(приранвивая производную к нуля мы находим возможные экстрэмумы, эти точки не всегда ими являются).
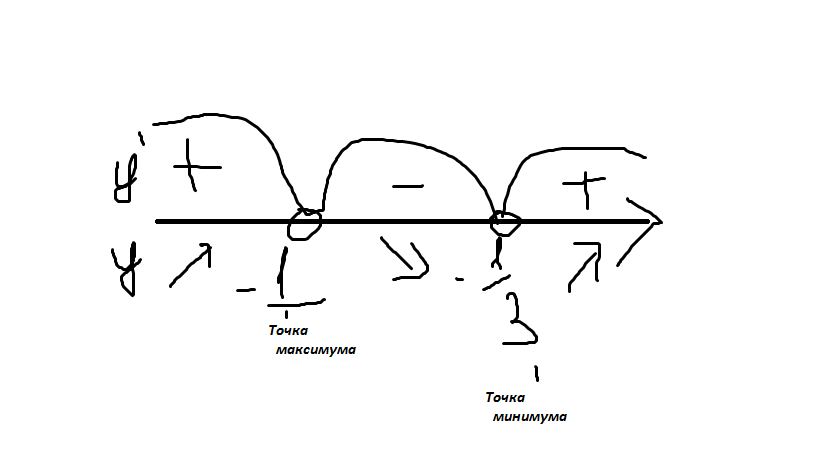
Начертим координатную прямую, нанесём нули производной, определим знаки на интервалах, промежутки убывания и возростанию функции(где производная положительная, там функция возростает. Отрицательная - убывает).
Далее вложение.
x=-1 - точка максимума функции.
х=-1/3 - точка минимума функции.
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад