Question

Найдите объём правильной треугольной пирамиды, сторона основания которой равно 4 корня из 3 (см), а боковое ребро - 5 см.

Answer 1

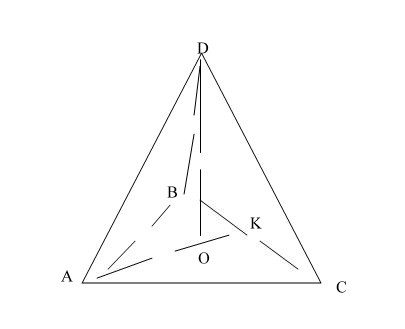
Дана правильная треугольная пирамида ABCD с высотой DO. В основании правильный треугольник АВС (АВ=ВС=АС= 4 корня из 3).

 

Рассмотрим треугольник АВС. Проведем высоту (медиану и бисс-у) АК.

ВК=КС= 2 корня из 3.

Рассмотрим треугольник АКС - прямоугольный.

AK^2 = AC^2 - KC^2

AK = 6

 

Медианы треугольник точкой пересечения делятся 2:1, считая от вершину. Высота падает в точку пересечения медиан.

АК=6, следовательно, АО = 4.

 

Рассмотрим треугольник AOD - прямоугольный.

DO^2 = AD^2 - AO^2

DO = 3

 

Vпир = 1/3 * Sосн * h

Sосн = 1/2 * ВС * АК = 12 корней из 3

Vпир = 1/3 * 12 корней из 3 * 3 = 12 корней из 3