при каких значениях параметра "p" уравнение x^2+(2p-1)x+p^2-1=0 имеет хотя бы один отрицательный путь?
Ответы
Ответ дал:
0
Чтобы уравнение имело хотя бы один отрицательный корень, дискриминант должен быть больше нуля:
Для отбора корней проверим условие D=0;
Заметим? что при p=1 уравнение не имеет отрицательных корней, значит это значение не входит в ответ.
Ответ:
Ответ дал:
0
Вы можете выложить решение? или места нету?
Ответ дал:
0
Понимаю вас, ну ладно, как модеры отправят на изменение решения, исправлю
Ответ дал:
0
Данное уравнение является квадратным.
1) Рассмотрим случай, когда свободный член равен нулю.

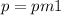
При р=-1 не имеет отрицательных корней.
не имеет отрицательных корней.
При р=1 имеет один отрицательный корень (х=-1)
имеет один отрицательный корень (х=-1)
2) Рассмотрим случай, когда второй коэффициент при х равен нулю, а свободный член не равен нулю, т.е. при :
:
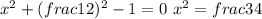
Это уравнение имеет корни разных знаков.
3) Рассмотрим случай, когда уравнение является полным.
Условие существования по крайней мере одного корня - это

а) Если у уравнения возможен единственный отрицательный корень, то
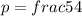 , тогда
, тогда  - отрицательный.
- отрицательный.
Если существует два корня, то
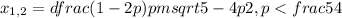
В таком случае оба корня могут оказаться отрицательными, но потребуем, чтобы отрицательным оказался меньший из этих корней:

Последняя система неравенств равносильна совокупности условий:
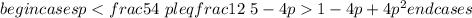 или
или 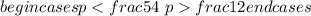
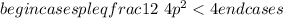 или
или 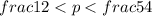
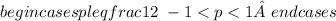
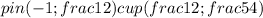
Итак,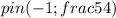
1) Рассмотрим случай, когда свободный член равен нулю.
При р=-1
При р=1
2) Рассмотрим случай, когда второй коэффициент при х равен нулю, а свободный член не равен нулю, т.е. при
Это уравнение имеет корни разных знаков.
3) Рассмотрим случай, когда уравнение является полным.
Условие существования по крайней мере одного корня - это
а) Если у уравнения возможен единственный отрицательный корень, то
Если существует два корня, то
В таком случае оба корня могут оказаться отрицательными, но потребуем, чтобы отрицательным оказался меньший из этих корней:
Последняя система неравенств равносильна совокупности условий:
Итак,
Вас заинтересует
2 года назад
8 лет назад
8 лет назад
11 лет назад
11 лет назад
11 лет назад