Question

Помогите пожалуйста! Решите задачу: Радиусы двух пепесекающихся окружностей равны 17см и 39см, а расстояние между их центрами 44 см. Найдите длину общей хорды окружностей. Решение желательно поподробней.

Answer 1

Алгоритм такой.

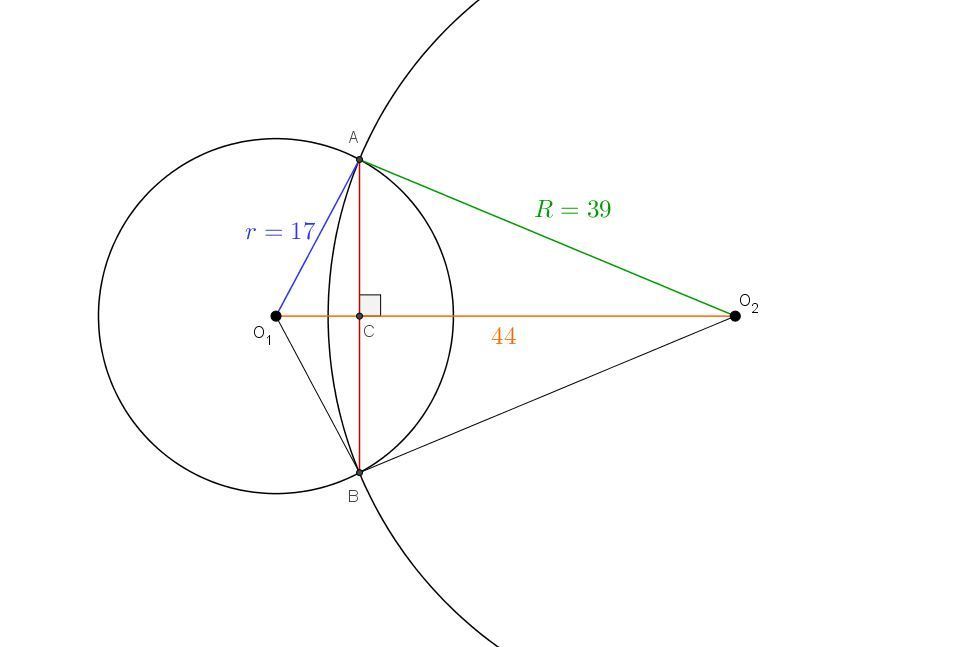
1) Строим чертёж (см. вложение)

2) Используем теорему о том, что общая хорда окружностей — то есть отрезок, проходящий через точки их пересечения, — перпендикулярна отрезку, соединяющему центры окружностей. Эту теорему доказывать нужно или можно использовать без доказательства? Вы её уже доказывали в школе?

3) Найдём площадь треугольника $O_1AO_2$ по формуле Герона:
 $p=(17+39+44)/2=50\S=sqrt{p(p-a)(p-b)(p-c)}=sqrt{50cdot33cdot11cdot6}=330.$

4) Согласно пункту 2, отрезок AC перпендикулярен стороне $O_1O_2$, а значит, является высотой нашего треугольника. Свяжем площадь, вычисленную по формуле Герона, с формулой площади через сторону и высоту:
$S=O_1O_2cdot AC/2=330\44cdot AC=660\AC=660/44=60/4=15$

5) Теперь рассмотрим треугольник $O_1O_2B$:
а) $O_1B=O_1A$ как радиусы малой окружности;
б) $AO_2=BO_2$ как радиусы большой окружности;
в) $O_1O_2$ — общая сторона.
Следовательно, треугольники $O_1AO_2$ и $O_2BO_1$ равны по трём сторонам, а значит, у них равны и высоты: $AC=CB=15$

6) Следовательно, искомый отрезок $AB=AC+CB=15+15=30$.

Ответ: $AB=30$(см).

Answer 2

Спасибо огромное! Очень помогли.

Answer 3

Пожалуйста.

Answer 4

Можно доказательство перпендикулярности