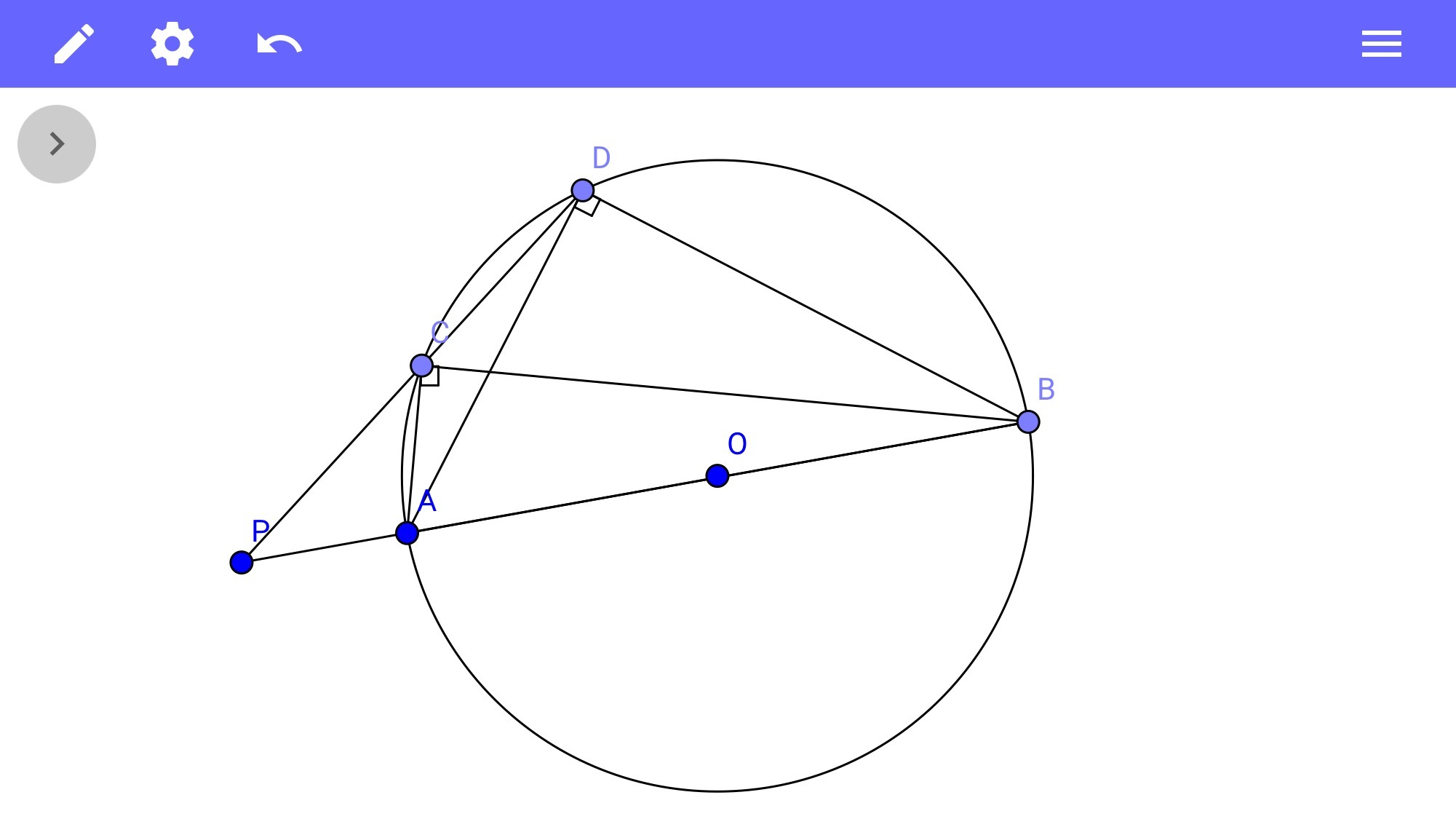
Прямоугольные треугольники ABC и ABD расположены по одну сторону от их общей гипотенузы АВ. Отрезки АВ и СD пересекаются в точке Р. Докажите, что треугольники АСР и ВDР подобны.
пожалуйста срочно сложно помогите
Ответы
Ответ дал:
0
Прямоугольные треугольники имеют общую гипотенузу, значит оба вписаны в одну окружность с диаметром АВ.
Для этой окружности РВ и РД - секущие.
По теореме о секущих РА·РВ=РС·РД, отсюда РА/РС=РД/РВ.
С таким отношением сторон и общим углом Р треугольники АСР и ВДР подобны.
Доказано.
Для этой окружности РВ и РД - секущие.
По теореме о секущих РА·РВ=РС·РД, отсюда РА/РС=РД/РВ.
С таким отношением сторон и общим углом Р треугольники АСР и ВДР подобны.
Доказано.
Приложения:
Ответ дал:
0
Спасибо большое
Вас заинтересует
2 года назад
2 года назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад