Question

Решите 3 легких тригонометрических неравенства. Молю это последнее задание и я получу оценку за семестр но я в них не разберусь. Сжальтесь и помогите.

Answer 1

task/24856782
---.---.---.---.---.---
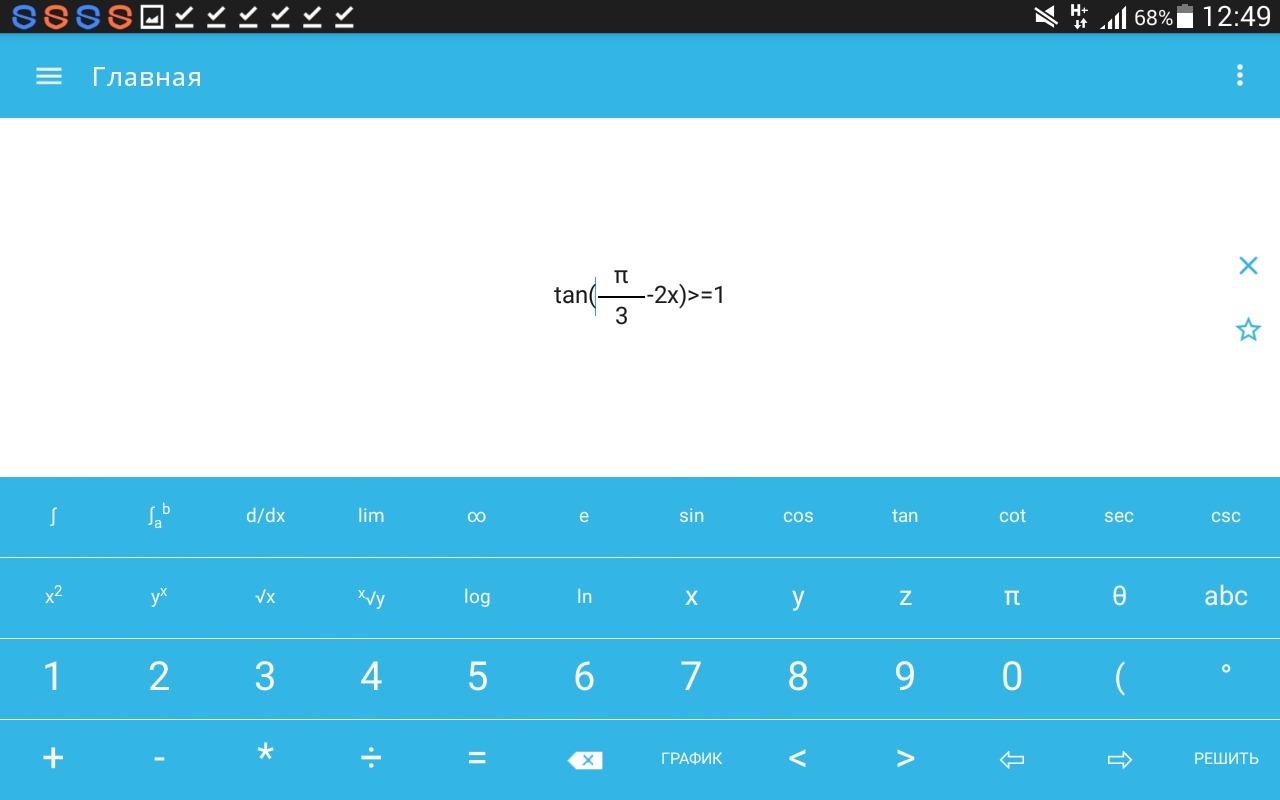
1)   tg(π/3 -2x) ≥1
tg(π/3 -2x)≥1⇔tg(-(2x -π/3) )≥1⇔ - tg(2x -π/3)≥1⇔ tg(2x -π/3) ≤  -1 ⇔
- π/2 +πn  <2x -π/3 ≤ arctg(-1) + πn ,⇔ - π/2 +πn  <2x -π/3 ≤ -π/4 + πn , n∈Z 
-π/2 +π/3+πn <2x  ≤ π/3 -π/4 + πn , n∈Z ;
-π/6 +πn  <2x  ≤ π/12 + πn , n∈Z ;
- π/12 +πn/2  <  x  ≤  π/24 + πn /2  , n∈Z .
∪ (-π/12+πn/2 ;π/24 +πn/2) 
n ∈Z
------------------------
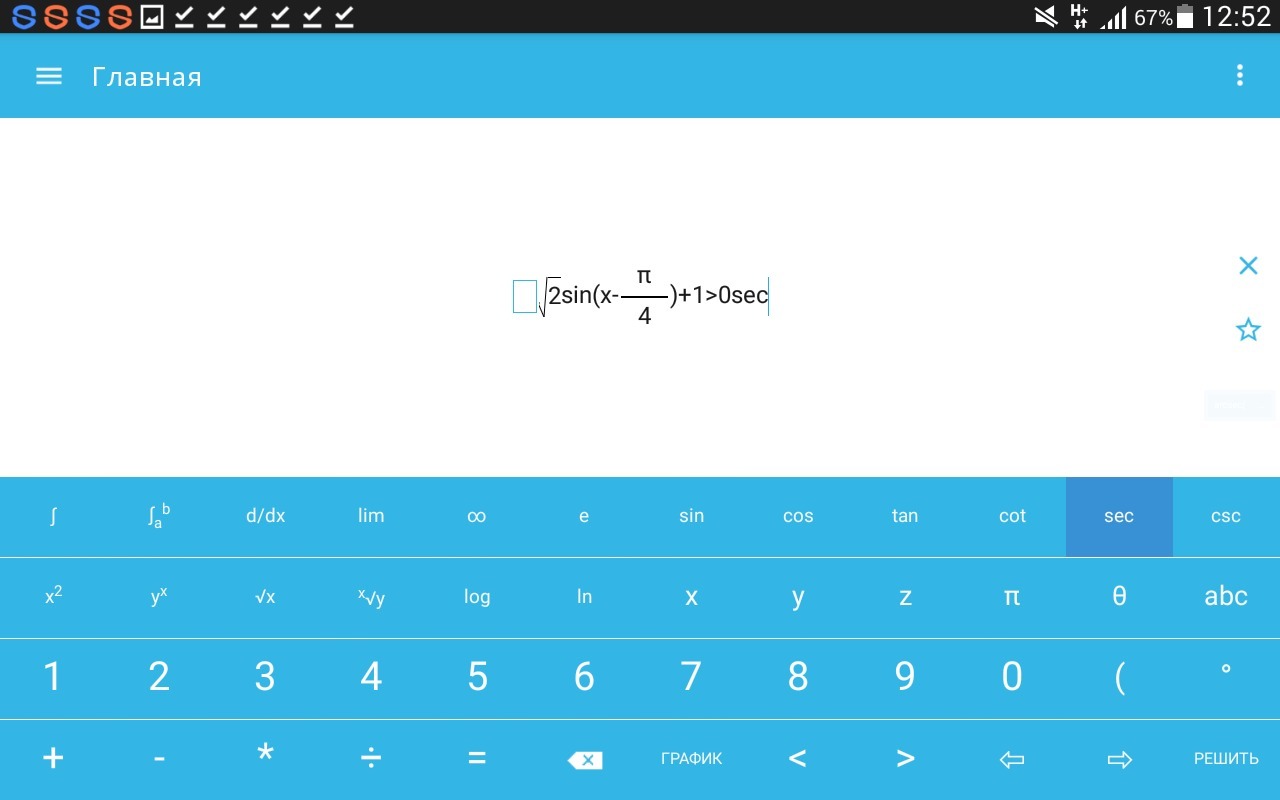
2)   √2sin(x -π/4) +1  > 0
√2sin(x -π/4) +1  > 0 ⇔  sin(x - π/4)  > -1/√2 ⇔
 arcsin(-1/√2) +2πn < x  - π/4  < π - arcsin(-1/√2) +2πn ⇔
- π/4+2πn <  x - π/4  < π -(-π/4)+2πn ⇔ 2πn < x < 3π/2 +2πn  , n∈ Z
------------------------
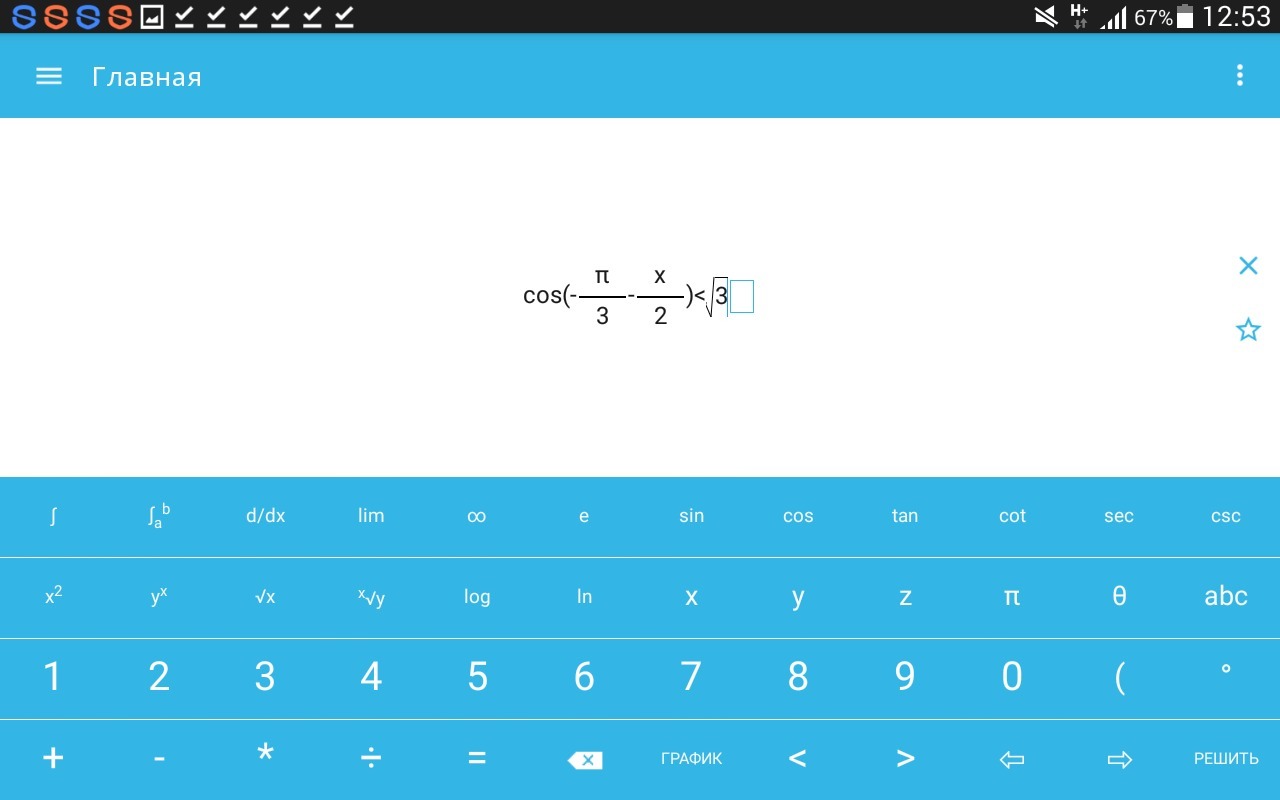
3₁)   если  cos( -π/3 - x/2) < √3  , то   x  - любое число 
------------------------
3₂)наверно   cos( -π/3 - x/2) < (√3)/2  ⇔ cos(-( x/2+π/3 ) ) < (√3)/2  ⇔
cos( x/2+π/3 ) <  (√3)/2  ⇔
arccos( (√3)/2 ) +2πn < x/2+π/3 < 2π -arccos( (√3)/2 ) +  2πn ⇔
π/6 +2πn < x/2+π/3 < 2π - π/6 +2πn ⇔ -π/6 +2πn <  x/2 < 3π/ 2 +2πn ⇔
- π/3 +4πn <  x <  3π +4πn  ,  n ∈ Z .