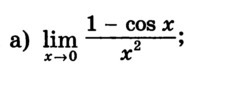Ответы
Ответ дал:
1
и не "заладится" ничего, здесь другой подход нужен.




 - первый замечательный предел
- первый замечательный предел


nclsgnv:
только разве в школьной программе есть замечательные пределы?
ну да
говорю тебе, нет там его
первый точно есть. как и неопределенности. хотя, насколько я помню, их мало освещают в школьном курсе
по крайней мере пролистав профиль за 10-11 классы я ни разу не встретил там упоминания о неопределенностях. и заметь, эта вот штука взята из задачника для школы
вконташке можем обсудить несовершенства школьной программы и простейшие пределы, которые, о ужас, оказались ее частью
простейшие. простеейшие. я сочту это за личное оскорбление
Ответ дал:
1
Можно и по правилу Лопиталя. Производная числителя sin(х), знаменателя 2x. Отношение в 0 не определено. Вторая производная числителя cos(x), знаменателя 2. Отношение при х=0 равно 1/2.
Ответ: 0,5
Ответ: 0,5
спасибо)
Вас заинтересует
1 год назад
1 год назад
2 года назад
2 года назад
3 года назад
9 лет назад