В окружности есть 3 хорды равные 12 см
Все 3 хорды пересекают друг друга и делят на 3 части
Также эти хорды образуют треугольник со сторонами 4, 5, 7
Проходит ли этот треугольник через центр или нет и почему
cos20093:
Ну не то чтобы прямо вот так значит. Если проекции точки на стороны треугольника лежат на сторонах, то СКОРЕЕ ВСЕГО точка лежит внутри треугольника :))) По крайней мере, я не могу придумать опровергающий пример
А как найти тогда эти отрезки не понимаю
Как сделать перпендикуляры к хордам? от какой точки их делать? всмысле высоту сделать или как?
Ага. здесь похожая история с вписанной окружностью. Я так раньше написал, что две равные хорды в окружности делят друг друга на пару равных отрезков. Поэтому можно написать так. x + y + 5 = 12; x + z + 4 = 12; z + y + 7 = 12; откуда и находятся эти отрезки
ну, центр окружности лежит на одинаковом расстоянии от концов хорд. Поэтому его (центра) проекция на хорду - это середина хорды. Если проекции точки (в данном случае - центра) на стороны треугольника лежат на сторонах, а НЕ на их продолжениях, то точка находится внутри треугольника.
Хм вроде понятно то есть нет шансов что центр лежит вне треугольника?
Это хороший вопрос.
лежит ли центр вне треугольника --это уже другая задача... а для этой задачи рассуждения могут быть следующими: если треугольник проходит через центр окр., то этот центр либо лежит на стороне треугольника, либо является вершиной треугольника, т.е. нужно рассмотреть 2 случая))
если центр лежит на стороне, то эта сторона--диаметр, а хорды равны (по условию), значит две другие стороны треугольника тоже диаметры (самые большие хорды), они пересекутся в центре--треугольника не получится... если центр в вершине треугольника, то тогда обе стороны--диаметры, вновь треугольника не получится... т.е. ответ на поставленный вопрос: нет, потому что равные хорды, проходящие через центр окружности --это диаметры окружности)
Уважаемый LFP:) Центр окружности не лежит на границе треугольника. Он лежит внутри него. Вопрос в задаче сформулирован с использованием неподходящего слова "проходит". Треугольники вообще-то никуда не проходят. А задача, лежит ли точка внутри треугольника, если проекции её лежат на сторонах - не должна быть сложной. И это хорошая задачка. Приглашаю вас поучаствовать в её решении.
Ответы
Ответ дал:
0
Возможны два случая:
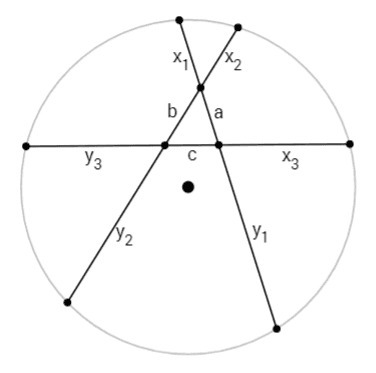
1) части хорд равны только при одной вершине треугольника.
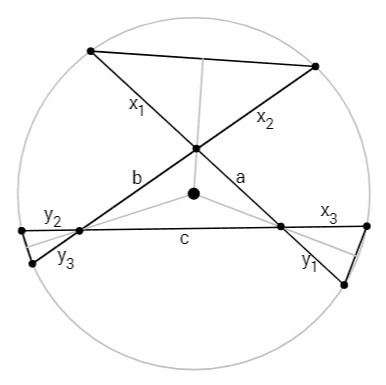
2) части хорд равны при трех вершинах.
В этом случае частями хорд образованы три равнобедренных треугольника, основаниями которых также являются хорды. Серединные перпендикуляры к хордам пересекаются в центре окружности. Также эти серединные перпендикуляры являются биссектрисами углов равнобедренных треугольников и равных им вертикальных углов данного треугольника. Точка пересечения биссектрис данного треугольника совпадает с центром окружности.
Обозначим части хорд:
x1+a+y1 = x2+b+y2 = x3+c+y3 =k
a=4; b=5; c=7; k=12
1)
x1=x2
x1+a=x3
x2+b=y3
x1+x2+a+b =x3+y3 <=> 2x1+a+b =k-c <=> x1= [k-(a+b+c)]/2
x1=(12-16)/2, но x1>0
Первый случай невозможен для данного треугольника.
2)
x1=x2
y1=x3
y2=y3
x1+x2+y1+y2+a+b =2k <=> 2x1+x3+y3 =2k-a-b <=>
<=> 2x1+k-c =2k-a-b <=> x1= (k-a-b+c)/2
x1=x2=5
y1=x3=3
y2=y3=2
Второй случай возможен для данного треугольника.
Точка пересечения биссектрис данного треугольника совпадает с центром окружности.
1) части хорд равны только при одной вершине треугольника.
2) части хорд равны при трех вершинах.
В этом случае частями хорд образованы три равнобедренных треугольника, основаниями которых также являются хорды. Серединные перпендикуляры к хордам пересекаются в центре окружности. Также эти серединные перпендикуляры являются биссектрисами углов равнобедренных треугольников и равных им вертикальных углов данного треугольника. Точка пересечения биссектрис данного треугольника совпадает с центром окружности.
Обозначим части хорд:
x1+a+y1 = x2+b+y2 = x3+c+y3 =k
a=4; b=5; c=7; k=12
1)
x1=x2
x1+a=x3
x2+b=y3
x1+x2+a+b =x3+y3 <=> 2x1+a+b =k-c <=> x1= [k-(a+b+c)]/2
x1=(12-16)/2, но x1>0
Первый случай невозможен для данного треугольника.
2)
x1=x2
y1=x3
y2=y3
x1+x2+y1+y2+a+b =2k <=> 2x1+x3+y3 =2k-a-b <=>
<=> 2x1+k-c =2k-a-b <=> x1= (k-a-b+c)/2
x1=x2=5
y1=x3=3
y2=y3=2
Второй случай возможен для данного треугольника.
Точка пересечения биссектрис данного треугольника совпадает с центром окружности.
Приложения:
Вас заинтересует
1 год назад
1 год назад
2 года назад
2 года назад
3 года назад
9 лет назад
9 лет назад