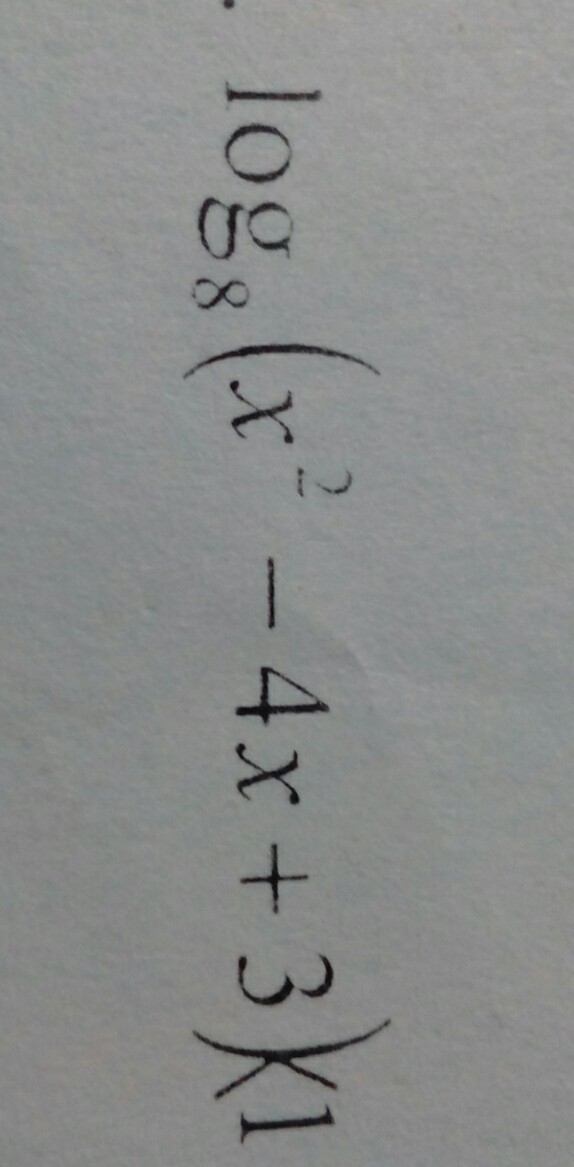Ответы
Ответ дал:
0
log₈(x² - 4x + 3) < 1
log₈(x² - 4x + 3) < log₈8
Решаем теперь систему из двух неравенств:
x² - 4x + 3 > 0
x² - 4x + 3 < 8
x² - 4x + 4 - 1 > 0
x² - 4x - 5 < 0
(x - 2)² - 1 > 0
x² - 4x + 4 - 9 < 0
(x - 2 - 1)(x - 2 + 1) > 0
(x - 2) - 3² < 0
(x - 3)(x - 1) > 0
(x - 2 - 3)(x - 2 + 3) < 0
(x - 3)(x - 1) > 0
(x - 5)(x + 1) < 0
x ∈ (-∞; 1) U (3; +∞)
x ∈ (-1; 5)
Пересекая оба неравенства, получаем общее решение:
x ∈ (-1; 1) U (3; 5).
Ответ: x ∈ (-1; 1) U (3; 5).
log₈(x² - 4x + 3) < log₈8
Решаем теперь систему из двух неравенств:
x² - 4x + 3 > 0
x² - 4x + 3 < 8
x² - 4x + 4 - 1 > 0
x² - 4x - 5 < 0
(x - 2)² - 1 > 0
x² - 4x + 4 - 9 < 0
(x - 2 - 1)(x - 2 + 1) > 0
(x - 2) - 3² < 0
(x - 3)(x - 1) > 0
(x - 2 - 3)(x - 2 + 3) < 0
(x - 3)(x - 1) > 0
(x - 5)(x + 1) < 0
x ∈ (-∞; 1) U (3; +∞)
x ∈ (-1; 5)
Пересекая оба неравенства, получаем общее решение:
x ∈ (-1; 1) U (3; 5).
Ответ: x ∈ (-1; 1) U (3; 5).
Ответ дал:
0
{x²-4x+3>0⇒(x-3)(x-1)>0⇒x<1 U x>3
{x²-4x+3<8⇒x²-4x-5<0⇒(x-5)(x+1)<0⇒-1<x<5
\\\\\\\\\\\\ ///////////////////////////
------(-1)---------(1)-----------(3)----------(5)---------
\\\\\\\\\\\\\\\\\\\\\\\\\
x∈(-1;1) U (3;5)
{x²-4x+3<8⇒x²-4x-5<0⇒(x-5)(x+1)<0⇒-1<x<5
\\\\\\\\\\\\ ///////////////////////////
------(-1)---------(1)-----------(3)----------(5)---------
\\\\\\\\\\\\\\\\\\\\\\\\\
x∈(-1;1) U (3;5)
Вас заинтересует
2 года назад
7 лет назад
9 лет назад
9 лет назад