Question

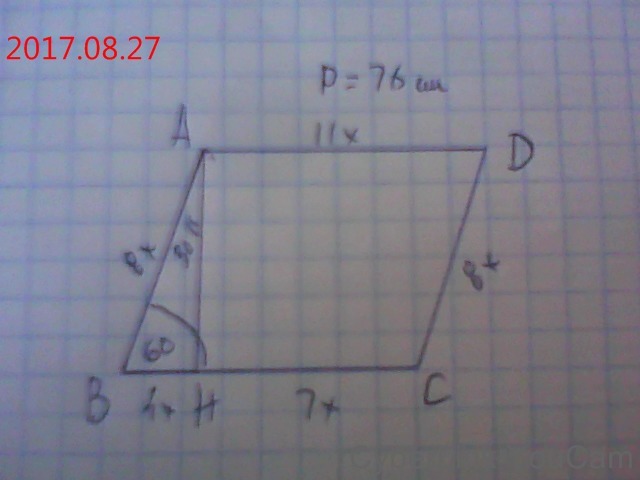
У паралелограма ABCD кут B дорівнює 60 градусів. Висота AH ділить сторону BC у відношенні 4:7 рахуючи від вершини гострого кута. Знайдіть сторони паралелограма якщо його периметр дорівнює 76 см

Answer 1

По умові АН⊥ВС. 
ΔАВН - прямокутний; ∠ВАН=30°. АВ=2ВН (катет проти кута 30°)
Нехай одна частина дорівнбє х, тоді за умовою ВН=4х; СН=7х;
ВС=АD=4х+7х=11х.
АВ=2ВН=2·4х=8х.
Периметр паралелограма Р=8х+11х+8х+11х=38х=76;
х=76/38=2.
Отже. АD=ВС=11х=11·2=22 см;
АВ=СD=8х=8·2=16 см.