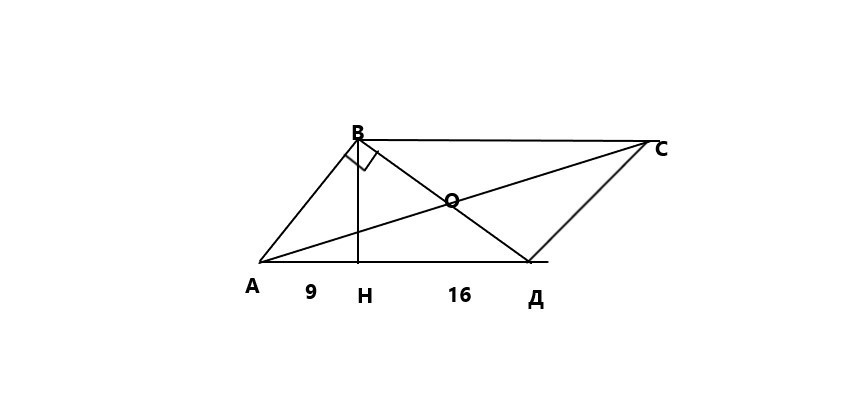
Меньшая диагональ параллелограмма перпендикулярна к его стороне, а высота, проведенная из вершины тупого угла, делит большую сторону на отрезки, равные 9 см и 16 см.
Найдите: а) стороны и высоту параллелограмма, проведенную из вершины тупого угла; б) диагонали параллелограмма; в) площадь параллелограмма.
Ответы
Ответ дал:
0
Меньшая диагональ параллелограмма перпендикулярна к его стороне, а высота, проведенная из вершины тупого угла, делит большую сторону на отрезки, равные 9 см и 16 см.
Найдите: а) стороны и высоту параллелограмма, проведенную из вершины тупого угла; б) диагонали параллелограмма; в) площадь параллелограмма.
Далее можно вычислить все что угодно.
Найдите: а) стороны и высоту параллелограмма, проведенную из вершины тупого угла; б) диагонали параллелограмма; в) площадь параллелограмма.
Далее можно вычислить все что угодно.
Приложения:

Ответ дал:
0
Треугольник АВД прямоугольный (по условию). Высота проведенная из вершины прямого угла равна квадратному корню из произведения длин отрезков гипотенузы на которые делит её высота.
h=√(9*16)=√144=12 см - высота параллелограмма;
9+16=25 см - одна сторона;
из треугольника АВН - АВ=√(9²+12²)=15 см - другая сторона;
из треугольника АВД ВД=√(12²+16²)= 20 см - одна диагональ;
из треугольника АВО АО=√(15²+10²)=√325= 5√13;
АС=2*АО=2*5√13=10√13 - другая диагональ;
25*12=300 см² - площадь.
h=√(9*16)=√144=12 см - высота параллелограмма;
9+16=25 см - одна сторона;
из треугольника АВН - АВ=√(9²+12²)=15 см - другая сторона;
из треугольника АВД ВД=√(12²+16²)= 20 см - одна диагональ;
из треугольника АВО АО=√(15²+10²)=√325= 5√13;
АС=2*АО=2*5√13=10√13 - другая диагональ;
25*12=300 см² - площадь.
Приложения:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад