Question

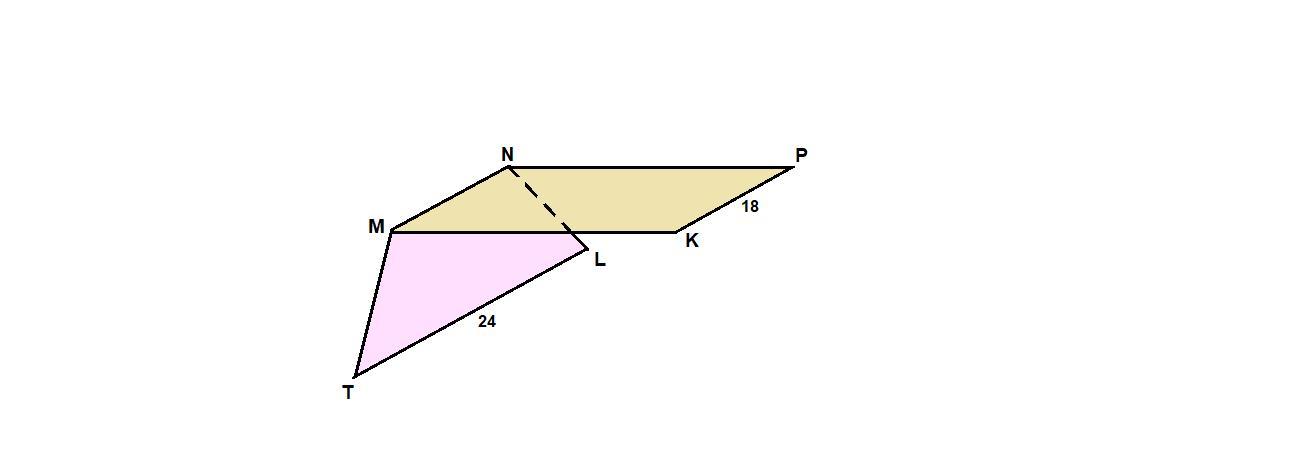
Даны паралелограмм MNPK и трапеция MNLT с основанием LT, не лежащим в одной плоскости. Выясните взаимное расположение прямых PK и LT. Найдите периметр трапеции, если в нее можно вписать окружность и PK=18см, LT=24см.

Answer 1

Ответ:

      PK ║ LT

      Pmnlt = 84 см

Объяснение:

PK ║ MN как противоположные стороны параллелограмма,

LT ║ MN как основания трапеции, ⇒

PK ║ LT (так как если две прямые параллельны третьей, то они параллельны между собой).

MN = PK = 18 см (противоположные стороны параллелограмма равны)

Если в трапецию можно вписать окружность, то суммы противоположных сторон равны:

MN + LT = MT + LN

Pmnlt = 2(MN + LT) = 2 · (18 + 24) = 2 · 42 = 84 см