Из двух пунктов, расстояние между которыми равно 18км, вышли одновременно навстречу друг другу две группы туристов и встретились через 2 часа. Определите, с какой скоростью шла каждая группа, если известно, что на прохождение всего пути одной из них потребовалось на 54 мин больше, чем другой.
Пожаааалуйста, уже крыша едет х.х Cистемой плз)
Ответы
Ответ дал:
0
54 мин = 54/60 = 9/10 = 0,9 часа
Скорость первой группы x км/ч, второй - y км/ч. За 2 часа навстречу друг другу прошли 18 км, то есть
(x+y)*2 = 18
или
x+y = 9
Первая группа прошла весь путь за 18/x часов, вторая за 18/y часов. Пусть вторая прошла весь путь на 0,9 часа быстрее, тогда
18/x-18/y = 0,9
Составим и решим систему уравнений:

Скорость первой группы x км/ч, второй - y км/ч. За 2 часа навстречу друг другу прошли 18 км, то есть
(x+y)*2 = 18
или
x+y = 9
Первая группа прошла весь путь за 18/x часов, вторая за 18/y часов. Пусть вторая прошла весь путь на 0,9 часа быстрее, тогда
18/x-18/y = 0,9
Составим и решим систему уравнений:
Приложения:
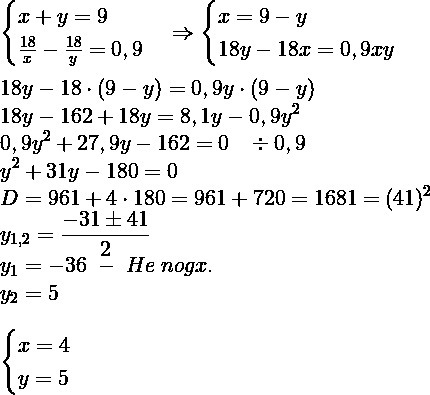
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад