Question

очень срочно нужно!!!

Answer 1

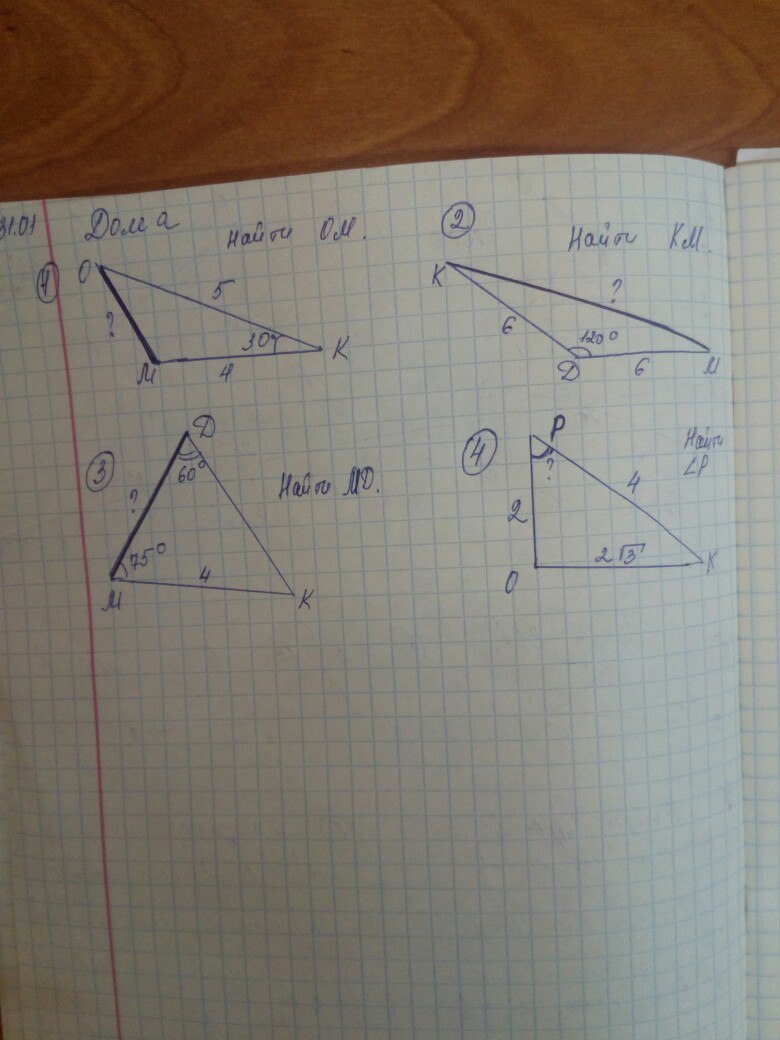
Все эти задачи на применение теоремы косинусов: если известны две стороны треугольника и угол между ними, то третья сторона вычисляется по формуле   с²=a²+b²-2abcosC

1) a=MK=4  b=OK=5  <C=30° c=M=√(16+25-40√3\2)=√(41-20√3)
2) a=b=6  cos120°=-sin30°=-0,5   c=√(36+36+36)=6√3
3) Здесь сперва необходимо найти недостающий угол =180-(60+75)=45° и вспомнить теорему синусов  4\sin60°=DK\sin75°  DK=4(sin75°\sin60°)
4)  cosP= (OX²-PO²-PX²)\2PO*PX   x=arccos(посчитанного выражения)