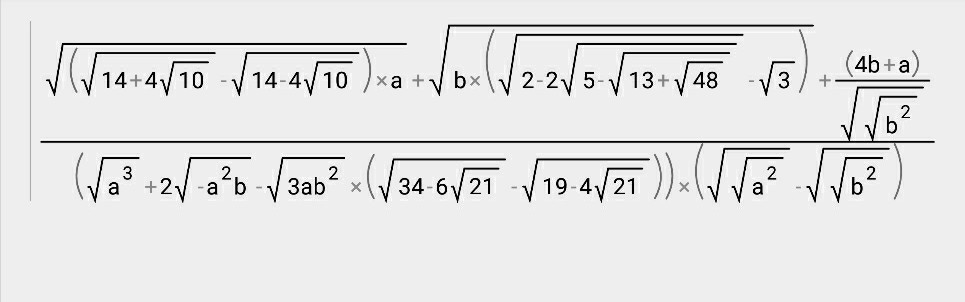Ответы
Ответ дал:
0
если найдете ошибку буду благодарна:
решаю по действиям
Числитель
1)

2)


3)

знаменатель
4)

5)

и теперь окончательная дробь

решаю по действиям
Числитель
1)
2)
3)
знаменатель
4)
5)
и теперь окончательная дробь
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад
10 лет назад