Question

Одна из двух окружностей проходит через центр другой окружности.Вычисли длину общей хорды , если радиус окружности равен 28 м.

Окружности и хорду,прилагаю

Answer 1

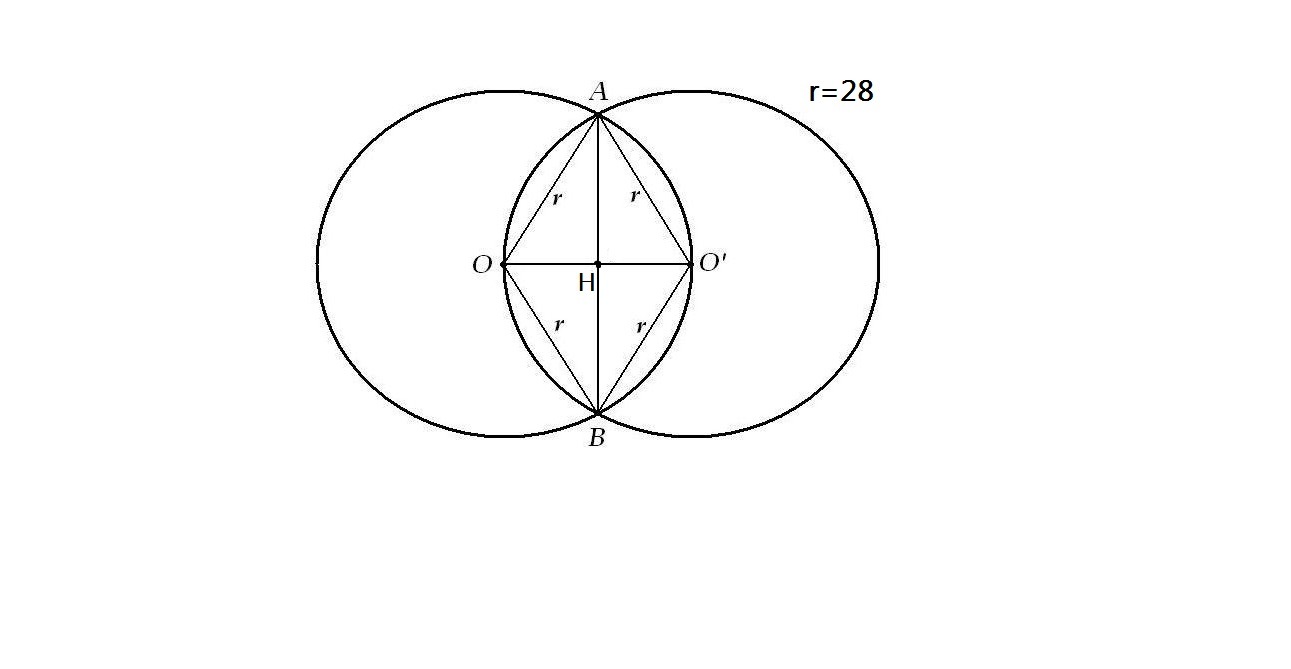
AOO'B - ромб с одиной диагональю равно радиусу окружности
т.е.
OO'=28
AB-другая диагональ, которую нам и нужно найти
AB=AH+HB
в равностороннем ΔOAO' AH-высота 
⇒ AH=(r√3)/2 = 28√3 / 2 = 14√3 
аналогично HB=14√3 
AB=(14√3 ) + (14√3 ) = 14√3 
Ответ: 14√3 

Answer 2

Ошибка записи. AB=(14√3 ) + (14√3 ) ≠ 14√3